L29-相似矩阵和若尔当形-习题集

参考

Unit III: Positive Definite Matrices and Applications - Similar Matrices and Jordan Form - Check Yourself
题源：Problem: Exercises on similar matrices and Jordan form | pdf
参考答案：Solutions: Exercises on similar matrices and Jordan form | pdf

问题 28.1

以下若尔当矩阵的特征值都是 $0, 0, 0, 0$ ，且都是具有两个（线性独立的）特征向量（每个若尔当块对应一个特征向量），但是从它们所划分得到的若尔当块并不相同，可以快速地判定它们不相似

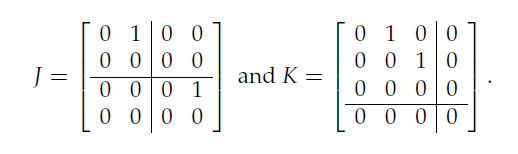
也可以通过分析使得等式 $JM=MK$ 成立的矩阵 $M$ 是一个不可逆矩阵，证明矩阵 $J$ 与矩阵 $K$ 不相似

解答

对于矩阵 $M$ 其中各个元素分别记作 $m_{ij}$

则等式 $JM=MK$ 的两边分别为

JM= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} {\color{Red} m_{11}} & m_{12} & m_{13} & m_{14} \\ {\color{Red} m_{21}} & m_{22} & m_{23} & m_{24} \\ {\color{Red} m_{31}} & m_{32} & m_{33} & m_{34} \\ {\color{Red} m_{41}} & m_{42} & m_{43} & m_{44} \end{bmatrix} = \begin{bmatrix} {\color{Red} m_{21}} & m_{22} & m_{23} & m_{24} \\ 0 & 0 & 0 & 0 \\ {\color{Red} m_{41}} & m_{42} & m_{43} & m_{44} \\ 0 & 0 & 0 & 0 \end{bmatrix}

KM= \begin{bmatrix} {\color{Red}m_{11}} & m_{12} & m_{13} & m_{14} \\ {\color{Red}m_{21}} & m_{22} & m_{23} & m_{24} \\ {\color{Red}m_{31}} & m_{32} & m_{33} & m_{34} \\ {\color{Red}m_{41}} & m_{42} & m_{43} & m_{44} \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & {\color{Red} m_{11}} & m_{12} & 0 \\ 0 & m_{21} & m_{22} & 0 \\ 0 & {\color{Red} m_{31}} & m_{32} & 0 \\ 0 & m_{41} & m_{42} & 0 \end{bmatrix}

当矩阵 $M$ 使得等式 $JM=MK$ 成立时，可得 ${\color{Red} m_{11}}=m_{22}=0$ 、 ${\color{Red} m_{21}}=0$ ， ${\color{Red} m_{31}}=m_{42}=0$ ， ${\color{Red} m_{41}}=0$

所以矩阵 $M$ 的第一列的元素都是 $0$ （不满秩），则矩阵 $M$ 是不可逆的

根据相似矩阵的定义，如果矩阵 $J$ 相似于矩阵 $K$ ，则必然存在一个可逆矩阵 $M$ 使得等式 $k=M^{-1}JM$ 成立。

但是从前面的推导可知，使得等式 $MK=JM$ 成立的矩阵 $M$ 是不可逆的，所以无法将等式转变得到 $k=M^{-1}JM$ 形式，所以矩阵 $J$ 与矩阵 $K$ 不相似。

问题 28.2

解释为什么以下论断都是正确的

如果矩阵 $A$ 相似于矩阵 $B$ ，则叫做 $A^{2}$ 也与矩阵 $B^{2}$ 相似
如果矩阵 $A^{2}$ 相似于矩阵 $B^{2}$ ，则矩阵 $A$ 可以不与矩阵 $B$ 相似
矩阵 $\begin{bmatrix} 3 & 0 \\ 0 & 4 \end{bmatrix}$ 与矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 4 \end{bmatrix}$ 相似
矩阵 $\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$ 与矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix}$ 不相似
将矩阵 $A$ 的第一行与第二行对调，然后再将第一列和第二列对调，得到矩阵 $B$ ，则矩阵 $A$ 与矩阵 $B$ 相似

解答一

如果矩阵 $A$ 相似于矩阵 $B$ ，则矩阵 $A$ 可以用 $B$ 表示为 $A=M^{-1}BM$

将以上等式代入 $A^{2}$ 可得

\begin{aligned} A^{2}&=A \cdot A \\ &=(M^{-1}BM)(M^{-1}BM) \\ &=M^{-1}B(MM^{-1})BM \\ &=M^{-1}BIBM \\ &=M^{-1}B^{2}M \end{aligned}

由于 $A^{2}=M^{-1}B^{2}M$ 则矩阵 $A^{2}$ 相似于矩阵 $B^{2}$

解答二

可以举出一个反例，例如矩阵 $A=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$ 和矩阵 $B=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}$

则矩阵 $A^{2}=B^{2}$ （它们的元素都是零），两个矩阵是相等的，所以它们必然是相似的，因为单位矩阵 $M=I$ 就可以使得等式成立 $A^{2}=M^{-1}B^{2}M$

但是不存在可逆矩阵 $M$ 使得等式 $B=M^{-1}AM$ 成立，由于任何矩阵与 $A$ 相乘都只能得到元素全为零的矩阵

解答三

矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 4\end{bmatrix}$ 的特征值是 $\lambda_{1}=3$ 和 $\lambda_{2}=4$

当特征值为 $\lambda_{1}=3$ 时，对应的特征向量为 $x_{1}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$
当特征值为 $\lambda_{2}=4$ 时，对应的特征向量为 $x_{2}=\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

由于矩阵具有两个线性独立的特征向量，则可以进行对角分解

其中特征向量矩阵是 $S=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$ 其逆矩阵是 $S^{-1}=\begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix}$ ，特征值向量是 $\Lambda=\begin{bmatrix} 3 & 0 \\ 4 & 0 \end{bmatrix}$

则矩阵可分解为

\begin{bmatrix} 3 & 1 \\ 0 & 4 \end{bmatrix} =S \Lambda S^{-1}= \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 3 & 0 \\ 0 & 4 \end{bmatrix} \begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix}

所以矩阵 $\begin{bmatrix} 3 & 0 \\ 0 & 4 \end{bmatrix}$ 与矩阵 \begin{bmatrix} 3 & 1 \ 0 & 4 \end{bmatrix}$ 相似

解答四

对于矩阵 $A=\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$ 可以将它分解为 $A=3I$

则对于任意可逆矩阵 $M$ ，等式 $M^{-1}AM$ 的值都是矩阵 $A$ 自身，由于 $M^{-1}AM=M^{-1}(3I)M=3M^{-1}IM=3M^{-1}M=3I=A$ 。

所以无法找到一个可逆矩阵 $M$ 使得矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix}=M^{-1}AM$ 成立

矩阵 $\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$ 与矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix}$ 不相似

提示

也可以根据相似矩阵的特性来进行推断，如果两个矩阵相似，则它们具有相同的特征值，而且线性独立的特征向量的数量也一样

分别求出两个矩阵的特征值，以及对应的特征向量

两个矩阵的特征值都是 $\lambda=3$

矩阵 $\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$ 具有两个线性独立的特征向量 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ 和 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$

但是矩阵 $\begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix}$ 只有一个线性独立的特征向量 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$

所以两个矩阵不相似

解答五

要将矩阵 $A_{n \times n}$ 的第一行和第二行对调，可以左乘一个置换矩阵 $P_{1, 2}$ （维度与目标矩阵 $A$ 相同，其作用是对目标矩阵的行向量进行交换）

P_{1, 2}= \begin{bmatrix} 0 & {\color{Red} 1} & 0 & \dots & 0 \\ {\color{Red} 1} & 0 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \\ \end{bmatrix}

而如果要将矩阵的第一列和第二列对调，则可以右乘一个转置的置换矩阵 $P_{1, 2}^{T}$ （其作用是对目标矩阵的列向量进行交换）

由于置换矩阵的逆矩阵是其转置矩阵，即 $P_{1, 2}^{-1}=P_{1, 2}^{T}$

观察矩阵 $P_{1, 2}$ 的结构特点，可知 $P_{1, 2}=P_{1, 2}^{T}$ ，所以 $P_{1, 2}=P_{1, 2}^{T}=P_{1, 2}^{-1}$

根据题意，矩阵 $B$ 可以表达为 $B=P_{1, 2}AP_{1, 2}^{T}$ 也可以写成 $B=P_{1, 2}^{-1}AP_{1, 2}$ ，所以矩阵 $B$ 与矩阵 $A$ 相似