L11-矩阵空间、秩 1 矩阵和小世界图
参考
矩阵空间 matrix space 是将矩阵「当作」向量,将一个个矩阵看作构成空间的基本元素,它们满足对于加法和数乘(即线性组合)的封闭性。
例如对于 是由所有 矩阵构成的矩阵空间,它和向量空间类似,有一些子空间,例如:
- 由所有对称矩阵 Symmetric Matrix 构成的空间
- 由所有上三角矩阵 Upper Triangular Matrix 构成的空间
- 由所有对角矩阵 Diagonal Matrix 构成的空间
根据向量空间维度的含义,表示/衡量向量里可以「自由取值」的元素(自由变量)的数量,所以矩阵空间的维度是指矩阵里可以「自由取值」的元素的数量。
上述 矩阵里各个元素都是可以「自由取值」(取任何值),因此由所有 矩阵构成的矩阵空间 ,其维度是
因此 空间的基由 个矩阵构成,例如以下列出的这些矩阵
说明
为了方便只列出了 个矩阵中的 个,其他矩阵可以按照规律写出
对于子空间 由所有的对称矩阵构成,对称矩阵中实际上只有 个元素可以「自由取值」的,剩余元素由于对称性的限制,只能基于另外的元素的指推导出,所以 空间的维度是
因此 空间的基由 个矩阵构成,例如以下列出的这些矩阵
对于子空间 由所有的上三角矩阵构成,上三角矩阵中实际上只有对角线和右上角的 个元素可以「自由取值」,剩余元素都只能是 ,所以 空间的维度是
因此 空间的基由 个矩阵构成,例如以下列出的这些矩阵
对于子空间 由所有的对角矩阵构成,对角矩阵中实际上只有对角线的 个元素可以「自由取值」,剩余元素都只能是 ,所以 空间的维度是
提示
对角矩阵即属于对称矩阵,也属于上三角矩阵,所以 空间也可以理解为 空间和 的交集
因此 空间的基由 个矩阵构成
说明
上述的子空间 、、 的基是空间 的基的子集,这种情况其实比较少见,一般而言,子空间的基并不取自原空间的基
其实可以将向量空间进行「泛化」推而广之,用其他元素取代向量,它们满足对相加和数乘操作的封闭(即对线性组合封闭),可以构建出更多类型的「空间」
例如对于在 空间且(或)在 空间的矩阵所组成的集合,即 ,并不能构成矩阵空间,因为很容易就会发现一个对称矩阵和一个上三角矩阵的线性组合可以得到任意的一个 矩阵,而这个矩阵并不一定是对称矩阵或上三角矩阵,所以 集合里的矩阵并不对线性组合封闭。
但是可以重新定义一种矩阵构成方式:一个对称矩阵加上一个上三角矩阵所得到的新矩阵作为基础元素,这样的矩阵构成的集合用符号 表示,这个集合可以构成矩阵空间,因为它和 其实是一样的,所以 空间的维度是
综合以上,可以得到一个父空间与子空间的维度关系等式
矩阵空间 由所有的 矩阵构成,那么由所有秩 的 矩阵组成的集合是否可构成子空间?
由这些矩阵组成的集合并不能构成一个矩阵空间,因为 的 矩阵对线性组合并不封闭。
提示
对于两个矩阵 之和 ,一般矩阵 的秩都比矩阵 或 的秩都要大
例如以下是两个秩均为 的矩阵 和矩阵
那么 得到的矩阵的秩为 (满秩)并不在集合中(因此集合中的元素对线性组合不封闭)
提示
除了将矩阵作为元素构成出矩阵空间,如果将零空间这个概念应用到微积分方程中,就可以将线性代数与微积分连接起来
对于以下微积分方程
它的一些特解如下
其通用解的表达式如下
微积分方程的解看起来不像是向量,但是它们也是由特解乘以系数,构成通用解的形式,所以这些解也是可以构成零空间(也适用于向量空间的概念),以上示例的零空间的维度是 ,因为它是由两个特解张成的
秩为 的矩阵,即矩阵只有一个主元
提示
在视觉上,秩为 的矩阵其简化阶梯形式 除了第一行,其他行元素为
例如 就是秩为 的矩阵
以上矩阵 各列都是线性相关的,所以秩
因此矩阵 的列空间 的维度是 ,则列空间 的基可以是矩阵 的第一列 ;而相应地,行空间 的维度是 ,则行空间 的基可以是矩阵 的第一行
其实对于秩 的矩阵,都可以「分解」为 的形式(其中 、 都是列向量,所以 是行向量)
提示
通过 相乘(其中 、 都是列向量,所以 是行向量)构成的矩阵,由于各行,以及各列都是线性相关的,所以矩阵的秩为
上面示例的矩阵 可以「分解」写成列向量 行向量的形式
说明
秩 1 矩阵就像是其他矩阵的积木一样。
例如对于 的矩阵,如果其秩 ,则只需要 4 个秩为 的矩阵(但是这些矩阵的主元所在的列不能相同)就可以(通过线性组合)构成原矩阵
假设在 向量空间中,向量 满足各元素(分量)之和为 ,则这些向量组成的集合 可否构成一个子空间?
提示
要判断向量集合是否可以构成一个向量空间,可以从向量空间的定义入手,即证明集合里的向量对线性组合封闭
根据上述的已知条件,可得集合 里的向量 满足
- 数乘:对于集合中的向量 与任意系数 通过数乘所得到的新向量 ,由于 所以 ,即新的向量 也满足各元素(分量)之和为 的约束,所以新的向量依然在集合 中。集合 中的向量对数乘操作封闭
- 相加:对于集合中的任意两个向量 和
由向量各元素(分量)之和为 可以得到下面的等式
所有由向量 和向量 相加构成的新向量 它的各元素之和也满足为 的约束 所以新的向量 依然在集合 中。
则集合 的任意向量的线性组合 ,由上面的分析可知数乘操作得到的新向量依然在集合 ,所以 和 属于集合 ,同样根据上面的分析可知相加操作得到的新向量也在集合 中,所以 与 之和得到的新向量也依然在集合 中,因此集合 中的向量对于线性组合封闭,因此该集合可以构成一个空间
向量空间 的维度只有 (而不是 ,虽然该空间里的向量有 个元素),由于向量的各元素满足 ,即可「自由取值」的元素(即自由变量)只有 个(剩下的一个通过等式关系推导出),所以维度
提示
关于向量空间 的维度的另一种求解思路:
可以将等式 看作如下
所以向量空间 是矩阵 的零空间
由于矩阵 的秩 所以 的维度是
图 graph 简写为 G 是指一系列通过线 edges 连起来的结点 nodes 的集合
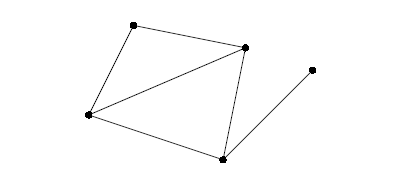 一个 graph
一个 graph
例如上面的图具有 5 个节点 nodes 和 6 条边 edges,可以用 的矩阵来表示
说明
小世界 small world 的由来:
六度分离猜想 six degrees of separation 认为则任何人都可以托一层又一层的朋友牵线,只需要约 6 步就可以认识任何一个陌生人,从这个猜想的角度来看,就会感觉世界「真小」。
如果将每个人看作是一个节点,朋友或熟人关系构成连线,则世界就可以构成一张图 graph,而这个图「最远」(指关系)的两个结点只需要 6 条线即可相连。
