L1-线性方程组的几何表示
线性代数的基本应用是解方程组,从几何的角度来看待线性代数和方程组的解。
参考
线性代数的基本应用是解方程组,对于 维方程组(有 个未知数和 个方程)可以通过三种观点/角度来求解:
对于一个二元方程组
将每个(每一行)方程的图像画出来就得到行图像,对于二元方程组,行图像中两条直线的交点的坐标就是方程组的解。
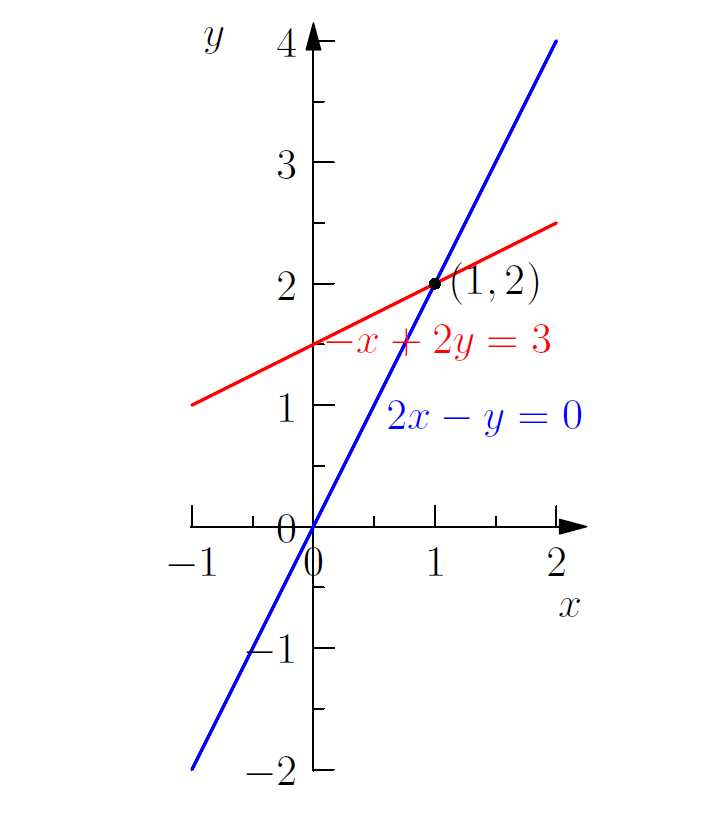 行图像
行图像
劣势
该可视化的解法对于高维度的方程组不太适用,由于高维度的图像无法在二维直角坐标系中直观绘出。
将方程组进行「向量化」,即把未知数的系数作为向量(列向量),把方程组等号右侧的数值作为目标向量,写出如下形式:
那么方程组的解(一组 和 的值)就是能够使这些列向量的线性组合等于目标向量的向量的倍数。
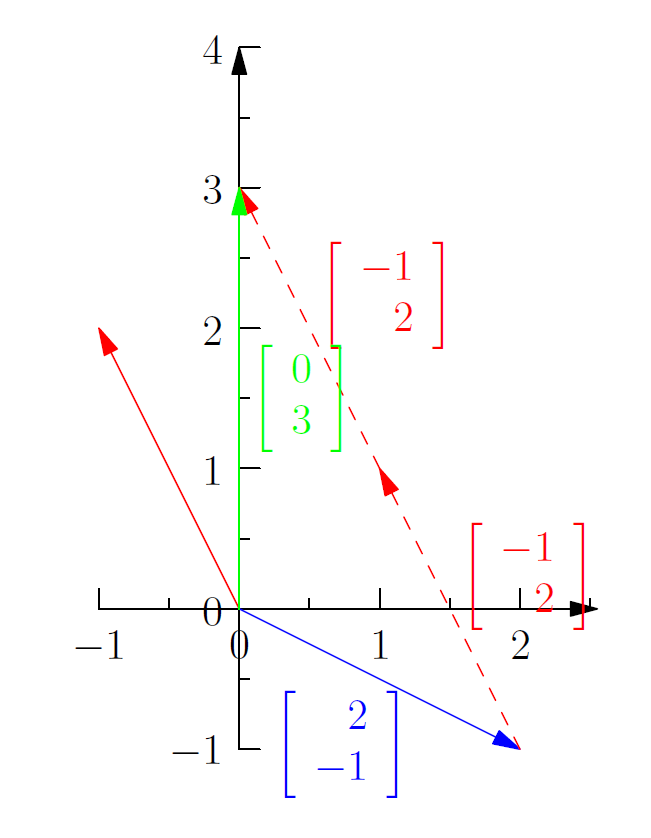 列图像
列图像
作出向量图,这就是列图像
 列图像
列图像
可以看出当 时,这样的向量的线性组合使等式成立
列图像实际是将方程组看作系数向量的线性组合 ,该方法可以扩展并适用于更高维的方程组。
其中 、 是二元方程组的对应系数所组成的列向量, 是目标向量,、 是方程组的未知数
可逆矩阵
可逆矩阵(非奇异矩阵 non-singular matrix)是指由方程组未知数的系数所组成的一系列列向量所构成的矩阵,这些列向量满足一个条件:
它们每个都是方向不同(不重合的),称为线性独立/不相关 linear independence
因此可以通过这些列向量的任意线性组合,实现所在维度的空间全覆盖
将方程组写成矩阵形式 ,公式中各参数的含义:
- 是由方程组的未知数对应系数所构成的矩阵 coefficient matrix
- 是由方程组的未知数构成的列向量
- 是方程组等式右侧(一系列值)所构成目标列向量
对于本文开头的方程组
它所对应的矩阵形式
提示
对于方程组的解 可以有两种方式理解,分别对应于 矩阵 向量 的两种运算规则:
- 列形式:将系数矩阵看作以列形式组合
- 行形式:将系数矩阵看作以行形式组合
一种理解方式是:将系数矩阵看作以列形式组合,则将未知数(即方程组的解)构成的向量看作是系数矩阵各列的线性组合的系数,因此将未知数向量的各数分别与矩阵相应列相乘,再相加,就可以得到目标向量
另一种理解方式是:将系数矩阵看作以行形式组合,将未知数(即方程组的解)构成的向量分别与矩阵相应行相乘(点乘),就可以得到目标向量
向量点乘规则


