L15-子空间投影
参考
- Unit II: Least Squares, Determinants and Eigenvalues - Projections onto Subspaces | pdf
- 课本章节:Read Section 4.2 in the 4th or 5th edition.
- 练习题:L15-子空间投影-习题集
Projection 投影在现实中是指将一个物体轮廓映射到一个平面上。
投影到直线
在直角平面坐标系中,将向量 投影到由向量 所指定的直线上,就是指在直线上寻找一个点,使得它与向量 的端点最近。
那么从直角坐标系的原点到这个点所代表的向量 ,就是向量 在直线上的投影
而由它们的差所得的向量 就称为误差
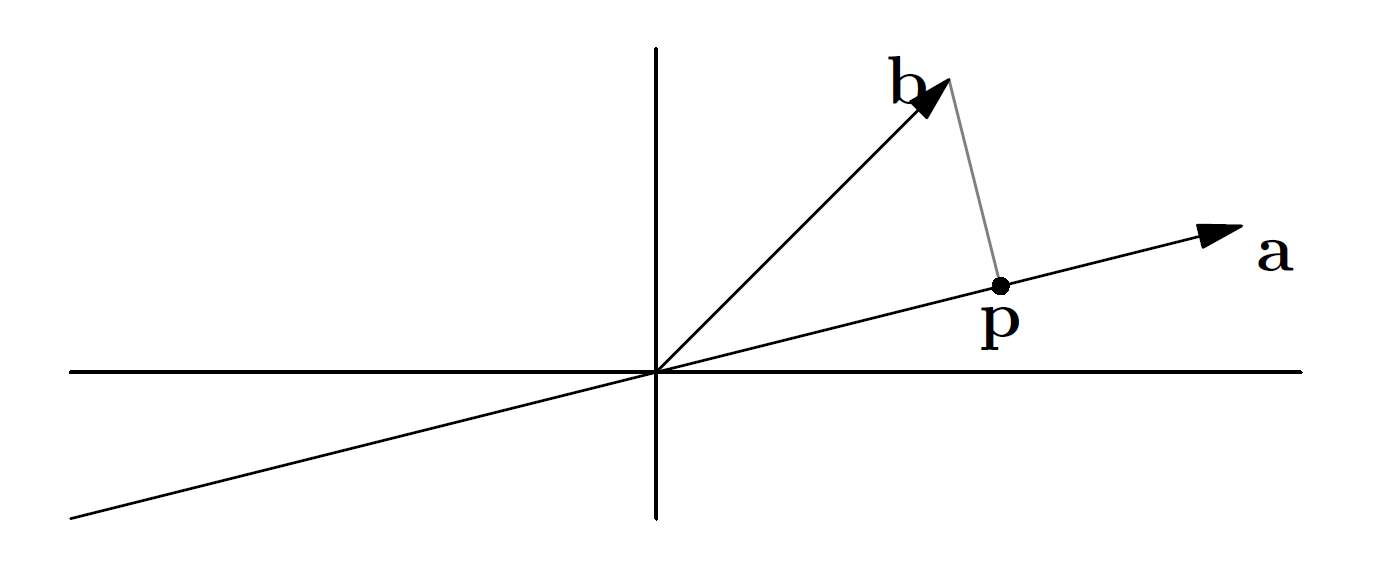
提示
可以将向量 理解为是 在向量 (所张成的空间)上的近似值。
而向量 就是近似值与原值的误差 error,在下文称它为误差向量
投影结果向量 在直线上,所以可以用向量 (的倍数)表示为
根据几何性质(点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离),误差向量 与向量 正交/垂直,根据向量正交的性质可知它们的乘积
以矩阵的形式表示
其中向量 和向量 都是列向量
提示
该(投影)规则可以推广到更高的维度
化简以上等式,由于在 等式中,根据向量相乘的规则可知 两个向量相乘的结果是一个数字(标量),所以可以进一步进行化简,最终求解得到系数 的值为
则投影结果向量 也可以写作 (因为 是系数,改变它与向量相乘的顺序不会影响结果)为
观察投影结果向量的构成式子(由向量 及其转置和向量 构成)可以得到以下特点:
- 当向量 改变时投影结果向量 也会随之改变,例如将向量 增大为原来的 2 倍,则投影也会改为 2 倍
- 当向量 改变时投影结果向量 并不会改变(该变动由于分式上下都存在 向量而相互「抵消」)
结合几何图形更容易理解,即将向量 的模长增长,那么它的投影也会变长;而改变向量 的模长,并不会影响其指定的直线,即投影位置并不变,所以投影向量也不变。
观察投影结果向量 其结构就像是一个矩阵作用于向量 使其映射到向量 上,得到投影结果 (小写),那么这个矩阵称为投影矩阵 (大写)
说明
投影矩阵 就是一个作用于向量 的矩阵(以相乘的方式)
将该向量 映射到目标空间中,得到投影向量
则投影矩阵 的值为
区别
投影矩阵 与投影结果向量 是不同的
投影矩阵 是用大写字母表示,而投影结果向量 是用小写字母表示的
另外需要留意的一点是,虽然投影矩阵 的分子分母由相同的元素构成,但是根据矩阵相乘的规则,不同的相乘顺序得到的结果也不同,分母是行向量与列向量相乘 得到一个数字(标量,其值等价于向量模的平方 ),分子 是列向量与行向量相乘得到一个矩阵,所以不可以对分式进行化简消去。
归纳总结
根据以上的推导得到 3 条关于(一维空间)向量投影的重要式子:
- 系数 (在投影结果向量 中的系数)
- 投影结果向量
- 投影矩阵
当投影矩阵 作用于向量 时(即与向量相乘 ,得到投影结果向量 ),以矩阵与列向量相乘的角度来考虑, 就是矩阵 的各列按照 进行线性组合,所以得到的结果向量 实际在投影矩阵的列空间 中。
因此对于任意向量 所对应的一系列 值就构成矩阵 的列空间,由于投影都会在(由向量 所指定的)直线上,所以矩阵 的列空间 的维度就是 ,即秩 ,而且向量 是该空间的一个基。
提示
根据《L11-矩阵空间、秩 1 矩阵和小世界图》这一节课的内容:
通过 相乘(其中 、 都是列向量,所以 是行向量)构成的矩阵,由于各行,以及各列都是线性相关的,所以结果矩阵的秩为
再结合投影矩阵的公式 其中 就是符合 结构,以矩阵与列向量(虽然 是一个行向量)相乘的角度考虑,就是 矩阵的各列根据 (的各列)进行线性组合,得到的矩阵(的列空间)依然在原矩阵 中。
投影矩阵 具有以下特性:
- 投影矩阵是对称矩阵
证明
投影矩阵 的式子中,分母两个元素相乘的结果是一个数字,所以考虑分子的 是否为对称矩阵即可
所以投影矩阵 是对称矩阵
- 投影矩阵的平方等于其自身
证明
因为 的作用是将向量 投影到向量 所在的直线上,那么投影结果向量 就在该直线上。
如果再将所得的向量投影到 所在的直线上 ,因为 本来就在直线上,所以(二次投影)结果依然得到第一次投影的结果向量,即
投影到平面
将投影的目标对象维度提高,由直线变成平面(即从向量变成矩阵),以探究更高维度的投影规律。
平面 由向量 和向量 张成。向量 并不在平面上,将该向量投影到平面上,投影结果向量是 。
由于平面是由(列向量)向量 和向量 构成的,所以可以用一个矩阵来表示 。
提示
因为这两个向量张成了平面,所以它们是线性独立的,那么该矩阵的列空间 的一组基就是由这两个向量 、 构成的。
由于向量 的投影向量 在平面上,所以投影向量可以用基向量来表示,即 ,也可以写成矩阵形式
提示
由于向量 的投影向量 在平面上,所以可以将投影过程理解为将向量「压在」在特定的空间中。
对于该示例,就是将向量 「压在」矩阵 的列空间中
那么误差向量 就是 ,因为误差向量与平面垂直,所以误差向量 也分别和该平面的一组基向量 、 正交,那么与它们的内积就是零,所以可以得到一组等式
其中向量 、、、 都是列向量
将以上的一组等式写成矩阵形式
可简化为
提示
观察 等式
其中 就是误差向量 ,所以等式也可以写成 ,即误差向量 在矩阵 的零空间 中,也可以理解为误差向量 在矩阵 的左零空间 中。
而根据矩阵的四个子空间的正交关系,左零空间 与列空间 正交,所以误差向量与列空间垂直 ,这也就表示误差向量与平面垂直,这也正是符合事实。
化简以上等式 得到
对比
投影到平面与投影到直线的场景类似,所以得到的方程式也是类似的
可以化简得到 因为其中的 是一个数字(标量),所以可以进行除法运算,最终可以求得
投影到平面化简得到 但是其中的 是尺寸为 的矩阵与尺寸为 的矩阵相乘,得到则是一个 的矩阵(而不是一个标量)
(无法直接进行除法运算)所以应该在等式两边乘上逆矩阵 进行化简
进一步求解可得系数 的值为
则投影结果向量 为
那么投影矩阵 (大写)就是
以上式子一般都不可以再进一步化简
注意
虽然根据相乘矩阵的逆矩阵的运算规则 可以将上面的式子进行化简,但是这个运算规则的前提是矩阵 和矩阵 自身都需要有相应的逆矩阵才成立,即矩阵 和 要是可逆才行
而在该示例中,矩阵 一般是一个长方形矩阵(行不满秩),即 是一个不可逆矩阵,所以一般无法对 进一步化简
假如矩阵 刚好是一个可逆方阵,那么投影矩阵 就正好是单位矩阵
在这种特殊的情况下,向量 的投影 就是其自身,因为投影结果向量在矩阵 的列空间中,也就是说向量 本来就在矩阵的列空间 中,那么矩阵 列满秩,其列空间本身就是包含了整个 空间
归纳总结
根据以上的推导得到 3 条关于(高维空间)向量投影的重要式子:
- 系数 (在投影结果向量 中的系数):
- 投影结果向量
- 投影矩阵
和投影到直线的投影向量一样,投影到平面的投影矩阵 同样具有以下特性:
证明
投影矩阵是对称矩阵
由于在 中, 本身就是一个 的对称矩阵,再根据相乘矩阵的转置的规则可以得到
该式子的转置与其本身相等,所以投影矩阵 是一个对称矩阵
证明
投影矩阵的平方等于其自身
可以从几何的角度来考虑,连续的两次投影的投影结果不变(因为第一次投影得到的向量就在目标空间中,而对目标空间中的向量进行投影,得到的结果等于其自身)
通过等式也可以证明
其中红色标记的部分的乘积为单位矩阵 ,所以最后可以得到
投影的应用
对于方程组 一般等式的数量都比较多,即系数矩阵 是一个长方形矩阵,这种情况下方程组一般是无解的,因为 的结果是在 的列空间中,但是 则不一定在列空间 中。
此时可以「改变」,通过最小的变动得到 ,使得 是在列空间 中,则对于 方程组,其解 就是最优解
这里的关键是怎最小的变动去「改变」 得到 ,其实就是通过投影的方式,即向量 就是向量 在矩阵 的列空间 的投影
课堂上介绍了一个使用场景:通过最小二乘法 Least Squared Fitting by a Line 求出一条直线,用于拟合一系列的点
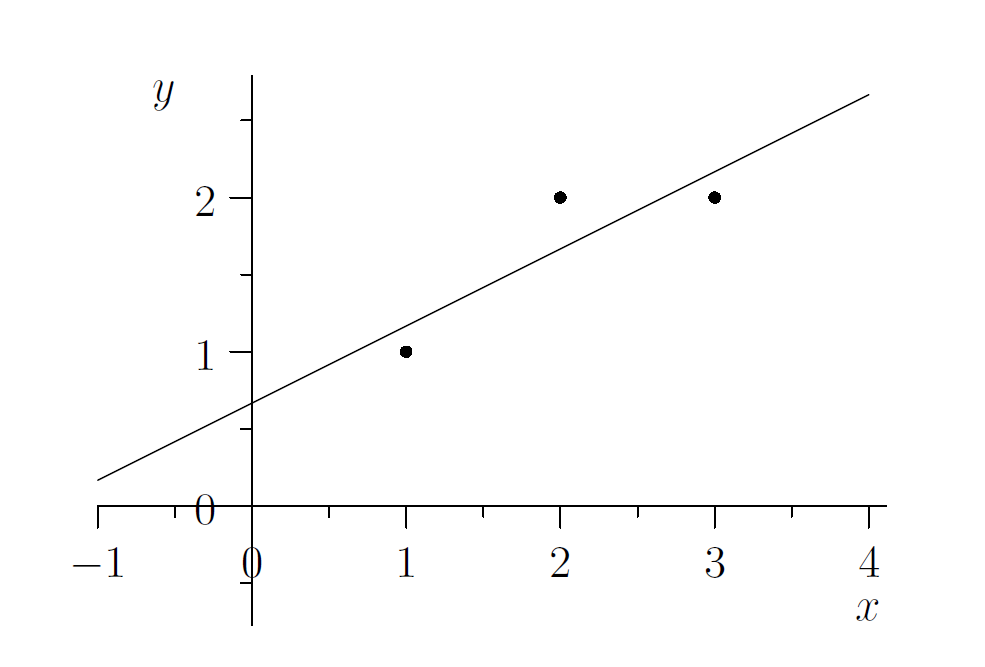
上图有三个点 、、 使用一条直线 对它们进行拟合,即求出 和 使得直线尽可能地接近这三个数据点
先假设这三个点都经过直线,将它们分别带入直线方程,可以得到一个方程组
以矩阵形式表示
但是实际上以上的方程组是无解的(可以通过化简或观察几何图像来判断,即无法找到一条直线完全经过 3 个点)
可以在等式两边乘上 使得系数矩阵方阵,则新的方程组可能有解(该解 就是原方程组的 最优解)