L28-正定矩阵和最小值
参考
以下是四个判定矩阵为正定矩阵的完整条件
说明
完整条件是指矩阵满足其中任何一个条件就可以证明是正定矩阵
所以这四个判定条件是平行等价的
- 特征值 均为正数
- 除了矩阵自身的行列式 为正数,沿着对角线向上的 个「子方阵」的行列式也都为正数
- 主元均为正数
- 对于任意向量 (除了 零向量),公式/函数 均为正数
最后一个判定条件更为常用
以 矩阵为例
当矩阵满足以下任意一个条件,则可证得它是正定矩阵
- 特征值的角度:、
- 行列式的角度:(左上角的矩阵 \begin{bmatrix} a \end{bmatrix}a>0ac-b^{2}>0$
- 主元角度:、
提示
可以用消元法来求出主元,将 作为第二列
也可以使用主元与行列式的关系(矩阵的行列式是其主元的乘积)来求解
矩阵的行列式为 根据
解得
- 特殊等式的角度:对于任意向量 (除了 零向量),等式 的值均为正数
对于以下 矩阵判定其正定性
从行列式的角度来判断, 处于正负数的「临界值」,将这种类型的矩阵称为半正定矩阵 semi-definite
从特征值的角度来判断,由于矩阵是奇异的( 列向量线性相关),所以必然存在一个特征值为 ,根据矩阵的迹与特征值的关系 可得 ,所以矩阵的特征值只有一个是正数的,并不是正定矩阵(而是半正定矩阵)
从 等式的角度来判断
将以上等式看作一个二元二次函数
提示
在等式 中,系数 为矩阵对应位置的元素
可以将以上等式看作是矩阵 的 quadratic form 二次形式
当该等式对于任意 都大于零,则矩阵 是正定矩阵;只要找出一组 使得等式为负数(存在反例),则矩阵 就不是正定矩阵
可以将等式进行配方,以便判断正负性 ,其中当等式为零时,其解除了 ,还可以有其他解,例如 ,所以原矩阵 不是正定矩阵(而是半正定矩阵)
除了对矩阵的二次形式(函数)进行配方,根据其结构推断函数值的正负,还有另一个更通用的方式,就是求出函数的最小值,将其与 比较,从而判断矩阵的正定性
注意
一般通过求导来寻找函数的最值。
要判断一个点是否为一元二次函数的极值点,需要同时考虑函数的一阶导和二阶导。当函数在该点的一阶导为零,且二阶导大于零时,该点就是函数的极小值点。
而对于多元二次函数,需要对各个变量进行求导,可以将不同变量的二阶导构成一个矩阵,例如对于 函数,将其二阶导 构成一个 矩阵
该矩阵称为 Hessian matrix 黑塞矩阵,该矩阵是一个对称矩阵,由于
当该矩阵是一个正定矩阵时,则它的行列式是正数,那么这些二阶导就满足 ,这对应于函数具有极小值的形式(从微积分的角度) ❓
对于高维度 的矩阵也是一样的,当函数 具有极小值时,则它所对应的 Hessian matrix 黑塞矩阵是一个正定矩阵
但实际上所求出的极值还需要谨慎地判断它是否为最值,此时可以结合函数的图像来进一步判断,这样也矩阵与几何相关联
对于以下 矩阵
其二次形式为 将其配方 ,并不是对于任意 函数值都是正数,例如当 时,函数值为负数
该函数的几何图像如下
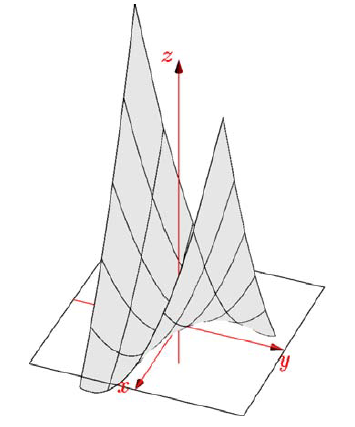 函数图像
函数图像
该函数呈马鞍形,在 处存在极小值,该点称为鞍点。如果令 ,则函数表示在 用一个平面对函数图像进行截断所得到的图像,该截面图是双曲线
观察以上的图像可知,函数有部分的图像位于 x0y 平面的下方(即位于 z 轴的负轴),对应的函数值为负数,所以原矩阵 不是正定矩阵
提示
也可以使用其他方式对矩阵的正定性进行判定
例如沿着左对角线的矩阵行列式依次为 、 原矩阵的行列式为负数,所以该矩阵不是正定矩阵
对于以下 矩阵
其二次形式为 将其配方 观察函数的结构,可知该函数的值都是大于 (除了 处函数值为 ),所以原矩阵是正定矩阵
提示
也可以使用其他方式对矩阵的正定性进行判定
例如沿着左对角线的矩阵行列式依次为 、 都是正数,所以原矩阵是正定矩阵
该函数的几何图像如下
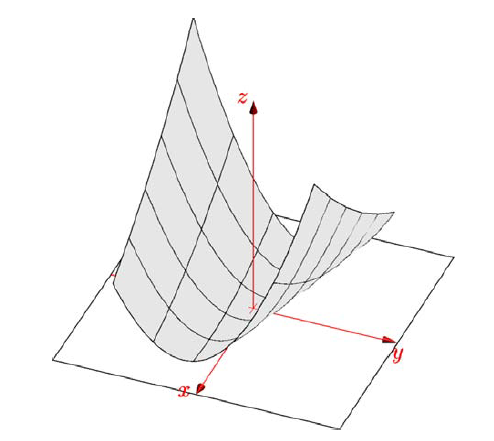 函数图像
函数图像
该函数呈碗形,在 处存在极小值,该点也是最小值。如果令 ,则函数表示的截面图是椭圆
说明
其实矩阵的二次形式的配方公式中,「外层」系数和「内层」系数和矩阵是有关联
配方形式是
这些系数出现在(使用消元法)求主元的步骤中
消元所得到的阶梯形式的矩阵是
将消元矩阵(相乘)结合起来所得的下三角矩阵是
以上通过颜色标记配方中的系数与矩阵元素的对应关系,矩阵的主元作为「外层」(平方项)的系数,消元时所称上的系数作为「内层」的系数
对于以下的 矩阵,可以使用不同的方法判断其正定性
- 从行列式的角度:沿着左对角线的矩阵行列式依次为 ,, 它们都是正数,所以原矩阵是正定矩阵
- 从主元的角度:该矩阵的主元为 都是正数,所以矩阵是正定矩阵
- 从特征值的角度:该矩阵的特征值为 都是正数,所以矩阵是正定矩阵
该矩阵的二次形式为 从前面的分析可知原矩阵是正定矩阵,所以除了在 处函数值为零以外,其他函数值都是大于零的。当在 对函数进行截断,所得导的是一个(三维的)橄榄球形状的截图(与 正定矩阵相对应,截面是一个椭圆)

