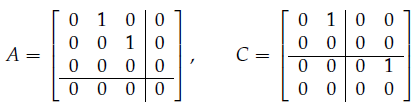L29-相似矩阵和若尔当形
参考
正定矩阵源自于最小二乘法,在该算法/求解步骤中出现了 ,其作用是将长方形的矩阵 构造/变成了 的方阵 这个方阵是半正定矩阵
证明
正是通过该公式 可以快速构建出一个对称矩阵,所以 的结果矩阵就是对称矩阵
再进一步分析其正定性
根据置换运算的规则,可以将 转换为 所以以上等式可以变成
其中 的结果是一个向量,即 实际是向量 模长的平方
因为 所以方阵 是半正定矩阵
如果矩阵 的零空间只有零向量,即方程 只有唯一解 ,那么对于 的任意向量, 成立,则 是正定矩阵
当矩阵 的零空间只有零向量,则表示矩阵各列向量是线性独立的,相对应地 是可逆的,则最小二乘法有最优解
对于正定矩阵 的逆矩阵 ,也是正定矩阵
证明
因为逆矩阵 的特征值是原矩阵 的特征值 的倒数 ,如果原矩阵 是正定矩阵,则它的所有特征值都是正数,相应地逆矩阵 的所有特征值也是正数,那么逆矩阵 也是正定矩阵
矩阵 和 都是正定矩阵,则它们的和 的结果矩阵也是正定矩阵
证明
如果矩阵 和 是正定矩阵,则对于任意向量 都满足
根据矩阵相乘法则(满足分配律)可得
所以矩阵 也是正定矩阵
如果存在一个矩阵 它具有可逆矩阵 ,使得 成立,则两个方阵 和 相似
使用以上等式,基于矩阵 ,采用不同的矩阵 就可以得到一系列的相似矩阵,这样就将一些矩阵联系起来,将它们归为一个族 family(类似于向量空间对线性运算封闭,该矩阵集合对 这个运算封闭❓),每个族内的所有矩阵彼此相似。每个族可以用一个对角矩阵(或结构与对角矩阵相似的矩阵)来表示。
例如对于矩阵 它的特征值是 和
由于它具有 个独立的特征向量,则可以进行对角化分解,得到 其中特征值矩阵 ,那么矩阵 相似于矩阵
以上是通过分解矩阵的方式来找到相似矩阵,还可以通过「逆向构造」的方式,找到相似矩阵
例如给出一个矩阵 其逆矩阵是 ,将它们相乘起来就可以得到与矩阵 相似的矩阵
通过计算可以知道矩阵 的特征值也是 和 ,它与矩阵 以及前面分解得到的特征值矩阵 都是相似的,而且它们的特征值都相同
根据特征值相同的这一特点,再根据 以及 ,可以快速构造出更多与 相似的矩阵,例如 、 等
其中特征值矩阵 是最特殊的,可以作为这一类相似矩阵的代表
相似矩阵都具有相同的特征值,且线性无关/独立的特征向量的数量也一样
证明
当矩阵 与矩阵 相似,则可以找到一个矩阵 满足等式
矩阵 的特征值 满足等式
将以上等式变形为
再在以上等式两边乘上矩阵 可得
将 替换上式等号的左边部分,可得
化简可得 即 也是矩阵 的特征值
但是矩阵 与矩阵 的特征向量并不完全相同(如果特征值相同,特征向量也相同,则矩阵就会相同)
存在一种特殊的情况,即矩阵 出现了数值相同的特征值(由于特征向量和特征值是成对出现的,相应地无法得到 个线性独立的特征向量),则矩阵 无法进行对角化(也就无法得到相应的对角矩阵 作为相似矩阵)
例如对于矩阵 它具有两个相同的特征值
⚠️ 那么由这两个特征值构成的对角矩阵 并不是与矩阵 相似,并不能和它归到一个族 family,这个特殊的对角矩阵(实际上是与单位矩阵呈倍数关系)是单独成为一类/族
因为对于任意可逆矩阵 ,公式 都是成立的,即它(对于该公式)是「自我封闭」的
而矩阵 与其他具有相同特征值矩阵归到另外一个族 family,例如 等,
若尔当 Jordan 提出了一种矩阵形式(和对角矩阵相似,更具有普遍性),以表示某一类的相似矩阵,可以包括具有相同的特征值的矩阵(而特征值矩阵 只能用来表示没有相同数值的特征值的矩阵),称作 Jordan Form 若尔当形
例如对于以上示例的一系列相似矩阵,其若尔当形是
对于以下的 的矩阵,它是一类相似矩阵的若尔当形
其特征值都是 秩为 ,所以零空间为 ,那么它的特征向量就「缺失」了两个(这里指的是特征向量线性相关,所以只有两个特征向量是线性独立的)
对于另一个矩阵,它具有相同的特征值,而且特征向量也是「缺失」两个,它与矩阵 相似
而考察以下矩阵
虽然它具有相同的特征值,而且特征向量也是「缺失」两个,但是它与矩阵 不相似
这里是根据矩阵可以划分的 若尔当块 Jordan Blocks 进行判定的
若尔当块 Jordan block 是一个矩阵 它在对角线上是重复的特征值,左下方元素都是 ,右上方紧挨着对角线的元素都是 ,其余都是
若尔当理论是指每一个方阵 都相似于一个若尔当矩阵 ,而这个若尔当矩阵是由若干个若尔当块 Jordan Blocks 构成的。可以对原矩阵按照若尔当块进行划分,如果两个矩阵是由不同的若尔当块构成的,那么即使它们矩阵相同的特征值和特征向量,也不能说明它们是相似矩阵
对于以上的矩阵 和 ,它们按照若尔当块进行划分,得到不同的结构,所以两个矩阵并不相似
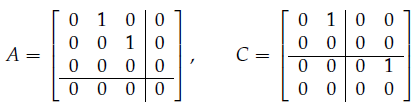 若尔当块
若尔当块
计算若尔当矩阵的思路
- 如果方阵 含有 个线性独立的特征向量,则它是可对角化的,那么它所对应的若尔当矩阵 是特征值矩阵(对角矩阵)
- 如果方阵 有 个重复的特征指,则相应地会有 个「缺失」的特征向量(这里指的是特征向量线性相关),则在若尔当矩阵 中将会有 个 位于对角元素的右上方