假设检验
假设检验是通常针对总体参数进行,而不是针对统计量的(因统计量是已经从数据(样本)中得到的,属于精确值,不需要假设测试验证这些数值)
步骤
主要由假设和检验构成,首先默认零假设为真,然后通过模拟计算试图证明为真的是备择假设
- 将问题转变为假设(零假设
Null,建立存在一定的主观性) - 收集数据,基于零假设,模拟针对一个统计量的抽样分布,构建置信区间
- 验证/检验(样本)数据中的特定统计量与模拟获得的(在特定置信度下)统计量是否一致,选择支持的假设(零假设 或备择假设 )。
验证假设的方法有两种:
- 利用置信区间选择(通过模拟统计量的抽样分布,观察事先作出的假设,挑选与抽样分布中观察到一致的假设)
- 传统方式是基于零假设(取等号时的情况)模拟会出现的情况,观察是否与(样本)数据一致
Tip
- 设置零假设和备择假设的规则
- 在收集数据前,预先设定 为真,通常零假设会表示某因素没有影响(效应为零)或对两组影响相同(两组同等)(包含等号)。
- 和 是竞争性(与零假设对立)、非重叠的假设。 可以证明为真(但需要 为假)。
- 包含一个等号,如 、 或
- 包含非空值 、 或
- 无论是在零假设还是在备择假设中,陈述时要避免出现接受这个词。我们并不是陈述某个假设为真,相反对于 I 类错误的阈值,你根据零假设中数据的相似性做出决定。所以,可以出现在假设检验中的措辞包括:
- 我们(有证据 的可信度)拒绝零假设。
- 我们(没有足够的证据)不拒绝零假设。
这样的描述有助于明确你最初零假设默认为真,并且如果没有收集数据,在测试最后「选择」零假设,是正确选择。
常见的假设检验
单样本 t 检验/测试总体平均数
T-Test (单样本 t 检验)
双样本 t 检验/测试均数差
Two Sample T-Test (双样本 t 检验)
python
import numpy as np, statsmodels.stats.api as sms
X1, X2 = np.arange(10,21), np.arange(20,26.5,.5)
cm = sms.CompareMeans(sms.DescrStatsW(X1), sms.DescrStatsW(X2))
cm.tconfint_diff(usevar='unequal')
配对 t 检验/测试个体治疗前后的差异
Paired T-Test (配对 t 检验)(常用于将个体与自己比较)
单样本 z 检验/测试总体比例
Z-Test (单样本 z 检验)
假设检验的错误
当我们基于样本作出假设选择,与实际现实不相符,则就发生了假设检验错误,存在两种假设检验错误。
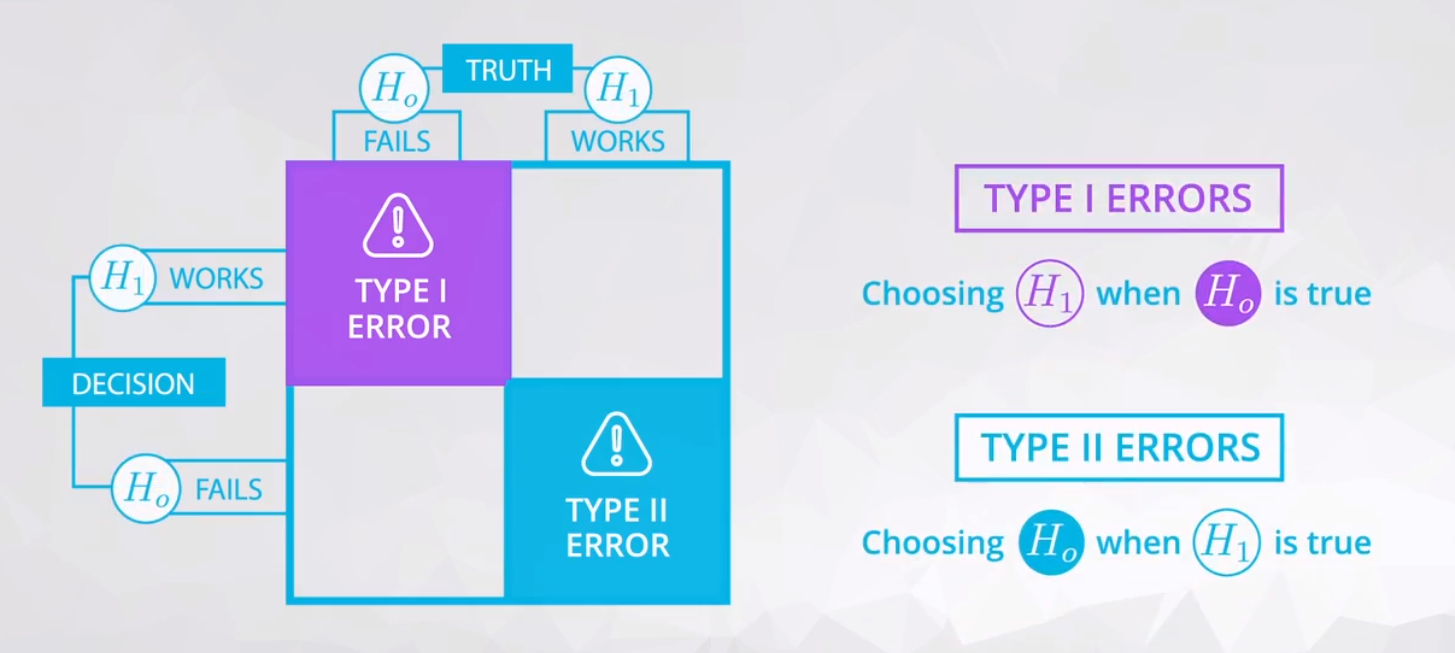
II 类错误 type 2 errors
二类错误或 错误是选择了零假设,但是备择假设为真( 为真时,认为零假设 为真)
即假阴性 false negative,II 类错误通常称为漏报
Warning
- 在一些极端情况下,我们通常选择一个假设 (如一直选择零假设),确保某个错误不再出现 (假设我们一直选择零假设,不再出现 I 类错误)。不过,一些单一的数据会降低某个错误类型的可能性,增加另一种错误类型的出现几率,两者是存在联系的。
- 实际设置中选择 I 类错误阈值,并且保证 I 类错误率符合要求后,可以最小化 II 类错误。
- 医学领域中常见的 I 类错误率 ,商业或学术研究中常见的 I 类错误率则为
- 如果完成多个假设检验,你的 I 类错误更加严重。为了纠正这点,通常采用邦弗朗尼校正法。这种校正法 非常保守,但是假如 I 类最新错误率应为实际想得到的错误率除以完成检验的数量。(如在 20 个(同样的)假设检验中把 I 类错误率维持在
1%,邦弗朗尼 校正率应为0.01/20 = 0.0005。你应该使用这个新比率,对比每 20 个检验的 p 值,做出决定。)避免出现复合 I 类错误的其他技巧包括: