概率

Prev Article Next Article

概率

通用法则

任何事件的概率在 0 和 1 之间，其中包括 0 和 1
互补事件的概率为 1 减去某个事件的概率
markdown
```
1−P(H)=P(not H)
```
其中 not H 可记为 $\neg H$
所有可能事件概率的总和等于 1
如果事件是独立的，一系列可能事件的（同时成立）概率是这些事件发生概率的乘积（而非独立事件的概率的计算可查阅条件概率）

概率质量函数 Probability mass function

Tip

参考：Probability mass function

概率和统计的异同

概率根据假定的模型或原因对未来事件做出预测（即预测数据）
统计中对发生的事件中的数据进行分析从而推断出这些模型或原因（利用数据进行预测）

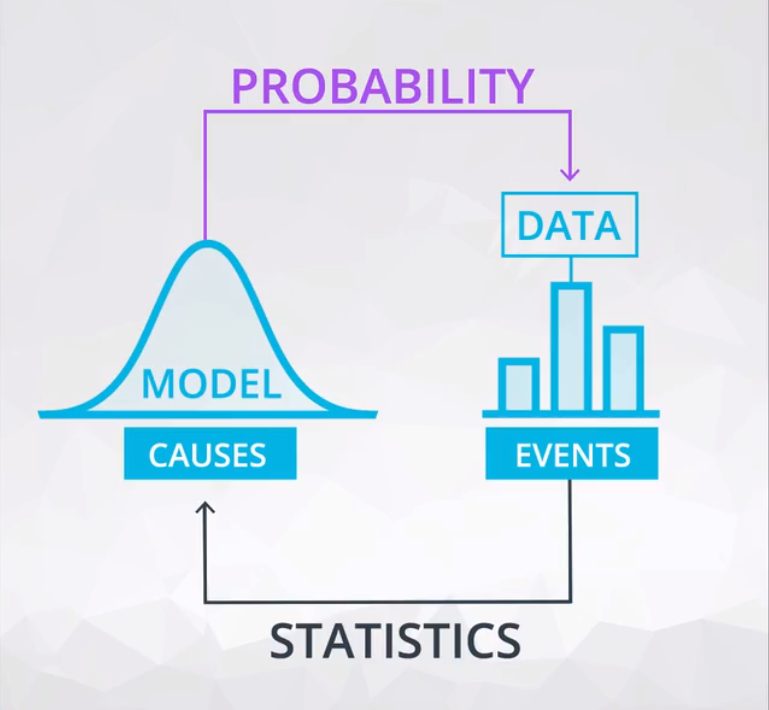概率与统计

条件概率

实际上，某个事件的结果依赖于之前的事件，该事件发生的概率为条件概率

任意两个事件的条件概率为：

P(A|B)=\frac{P(A\text{ }\cap\text{ }B)}{P(B)}

其中 $|$ 代表「鉴于/基于」， $\cap$ 代表「和」

如阳性检验测试结果的概率依赖于你是否具有某种特殊条件/前提（如是否患病）而不同

P(positive|disease)=\frac{P(positive\text{ }\cap\text{ }disease)}{P(disease)}

贝叶斯法则

贝叶斯定理（贝叶斯公式）能够告知我们如何利用新证据修改已有的看法。这个名称来自于托马斯·贝叶斯。

贝叶斯定理是关于随机事件A和B的条件概率的一则定理，一般事件A在事件B（发生）的条件下的概率 $P(A|B)$ ，与事件B在事件A（发生）的条件下的概率 $P(B|A)$ 是不一样的。

P(A|B)=\frac{P(B|A)P(A)}{P(B)}

Announce

$P(A|B)$ 是已知事件 B 发生后事件 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
$P(A)$ 是事件 A 的先验概率（或边缘概率）（之所以称为「先验」是因为它不考虑任何 B 方面的因素）
$P(B|A)$ 是已知事件 A 发生后事件 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
$P(B)$ 是事件 B 的先验概率（或边缘概率）

Previous Article

正态分布

Next Article

抽样分布

Copyright © 2024 Ben

Theme BlogiNote

Icons from Icônes