L6-列空间和零空间-习题集
参考
假设 和 都是向量空间 的子空间
- 定义: 是包含所有 组合的向量集合,其中 在子空间 中, 在子空间 中。求证: 是一个向量空间(满足对于线性组合封闭)
- 如果 和 都是 向量空间中的一条直线,那么 和 的区别是什么。(即解释 是由 张成得到的)
假设 是子空间 的向量, 是子空间 的向量,则有
根据向量空间对于向量的加法的封闭性,可得 和
所以 即 对向量的加法封闭。
类似地,根据向量空间对于向量的数乘的封闭性,可得 和 ,其中 是常量,所以
所以 对于线性组合封闭。
当 和 是两条不同的直线时,则根据 的定义,该向量集合的几何形式是一个平面;而根据 的定义,该向量集合的几何形式仅是两条直线。而 张成的空间是两个向量 和 的所有可能的线性组合,即 ,其中 是在直线 上, 是在 上。
所以 是由 张成得到的。
已知目标平面 与平面 平行,其中向量 在目标平面上。
则在目标平面上的点具有以下模式,请填充完整:
两平面平行,且平面 过原点 ,而点 在目标平面,因此从几何角度考虑,目标平面上的点可以将平面 上的点沿 轴移动 12 个单位得到相应的点。
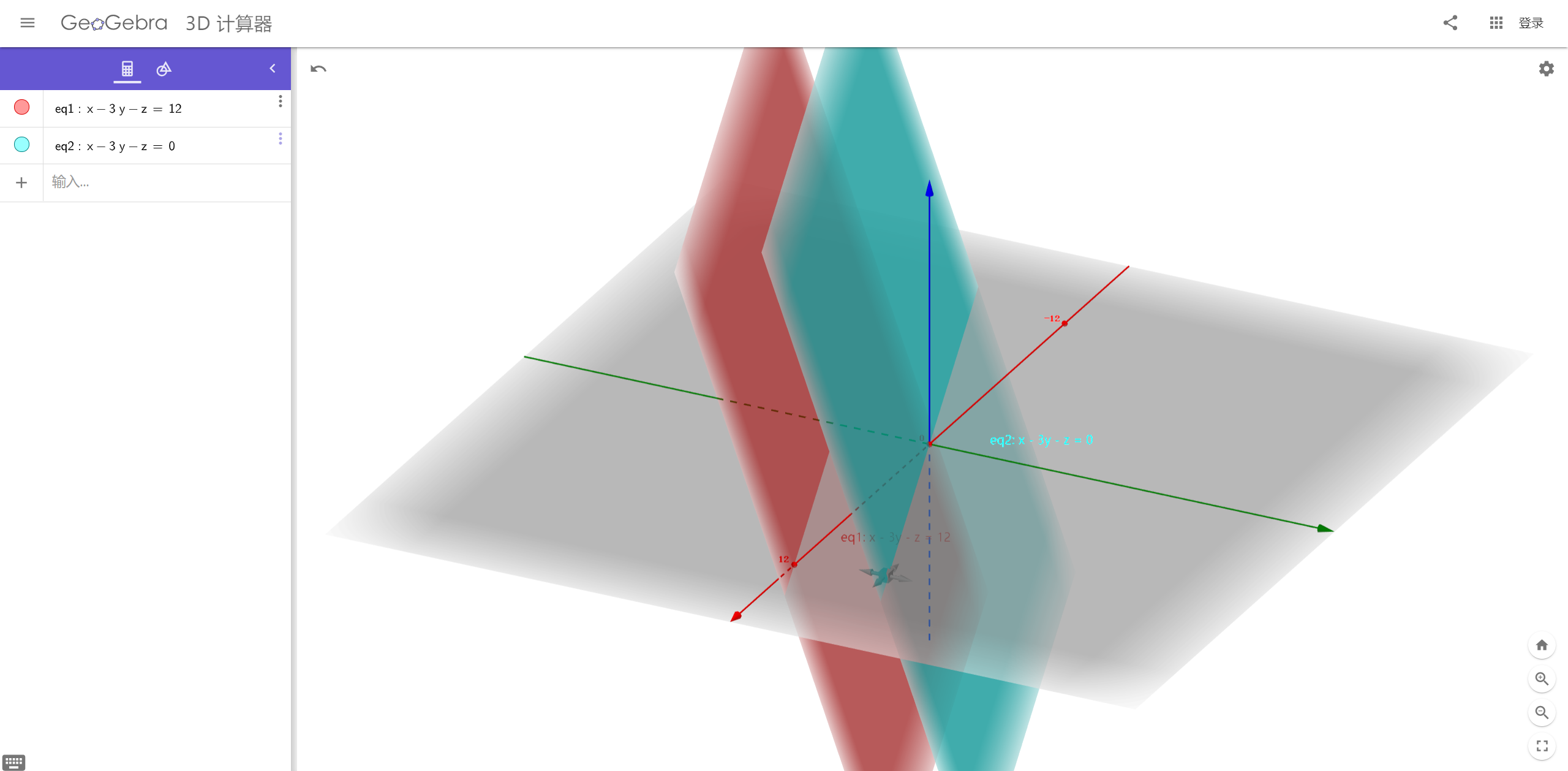 使等式成立的向量集合的几何表示
使等式成立的向量集合的几何表示
以矩阵的角度考虑,其中 是目标平面上的点, 是平面 上的点:
将平面(方程组) 写成矩阵形式
这些向量都可以使方程组 成立,则平面上的点构成零空间 ,根据题目的提示可以写出其中两个向量 和
可以将这两个向量作为基向量 basis 写出零空间向量的一般形式
而题目要求的形式则是将解进行「分解」,消去
即
因此可得
直接使用换元,并将写成矩阵形式
若向量空间 由向量空间 和 构成,且满足 ,求它们的零空间 和 与 的关系。
已知 则对于方程组 的所有解构成的零空间 ,需要满足 ,即这些解 需要同时满足 和 ,所以
