L8-求解 Ax=b 简化行阶梯形式
参考
这一节主要内容是 的求解步骤:
- 判断方程组的可解性 solvability
对于方程组
| 秩 | 系数矩阵的简化行阶梯形式 | 解数量 | 解形式 |
|---|
| 列满秩 | | 1 个或 0 个 | |
| 行满秩 | | 无限 | |
| 方阵满秩 | | 有且只有 1 个 | |
| 不满秩 、 | | 0 个或无限(由 决定) | |
- 求出特解 particular solutions :课程中所取的特解是在所有自由变量设为 的情况下,再求出主变量
- 求出零空间 ,作为基础解系 special solutions
- 这样就可以得到方程组(当有解时)所有解的形式
已知方程组 如下
写成矩阵的形式
提示
观察可知 row3 = row1 + row2,即系数矩阵第三行与第一、二行线性相关,因此当方程组有解时,右侧应该满足
使用消元法求解方程组 需要构建增广矩阵
当方程组有解时(三个等式都满足),由最后一行得到 成立,即
若取
则增广矩阵为
提示
其中第一列、第三列是主列 pivot column
使用消元法求解方程组 ,其可解性 solvability 可以从方程组右侧的 向量考虑:
- 列角度:将 看作是系数矩阵 各列基于 的线性组合,如果这个角度考虑,那么当方程组有解时,则 必须在系数矩阵 所构成的列空间 中
- 行角度:若系数矩阵 在消元过程中存在某行各元素均为零,则相应地在增广矩阵中该行的 的组合也要是零
为了便于讨论方程组的可解性,引入秩 这一概念(它是指在阶梯形式的矩阵中,矩阵的主元数量)
满秩 full rank 指各行或各列上都有主元,对于矩阵 有两种情况:
- 当 时,列满秩
- 当 时,行满秩
当秩满足不同条件时,方程组有不同的解。
当列满秩 时,每一列都有一个主元,则没有自由变量,即自由变量的自由度为 ,即零空间的维度是零(几何形式是一个点)
例如对于方程组
消元法求解方程组(为了演示简便,增广矩阵省略 部分)
通过系数矩阵的简化行阶梯形式可知,该方程组是否有解(唯一解),取决于变换后的增广矩阵第三、第四行是否成立,这与 相关。
所以当系数矩阵是列满秩 时,方程组 有 0 或 1 个解。如果存在唯一解 unique solution,其形式是
当行满秩 时,每一行都有一个主元,则自由变量的自由度为
例如方程组
消元法求解方程组(为了演示简便,增广矩阵省略 b 部分),在系数矩阵的简化行阶梯形式中 表示自由变量所对应的系数
根据 L7-求解 Ax=0 主变量和特解 这一节可知方程组 的零空间是 ,(通过确定自由变量的值后)可以方便地得到 所有解的形式是
此时方程组 必有解,且是无限个,其形式是 。
其中 表示方程组 的解所构成零空间 ,它作为基础解系,只需要再结合方程组 其中任意一个特解 (可以将该特解的作用看作是一个平移向量,将方程组 的解所构成零空间 平移到方程组 的解构成的向量空间)
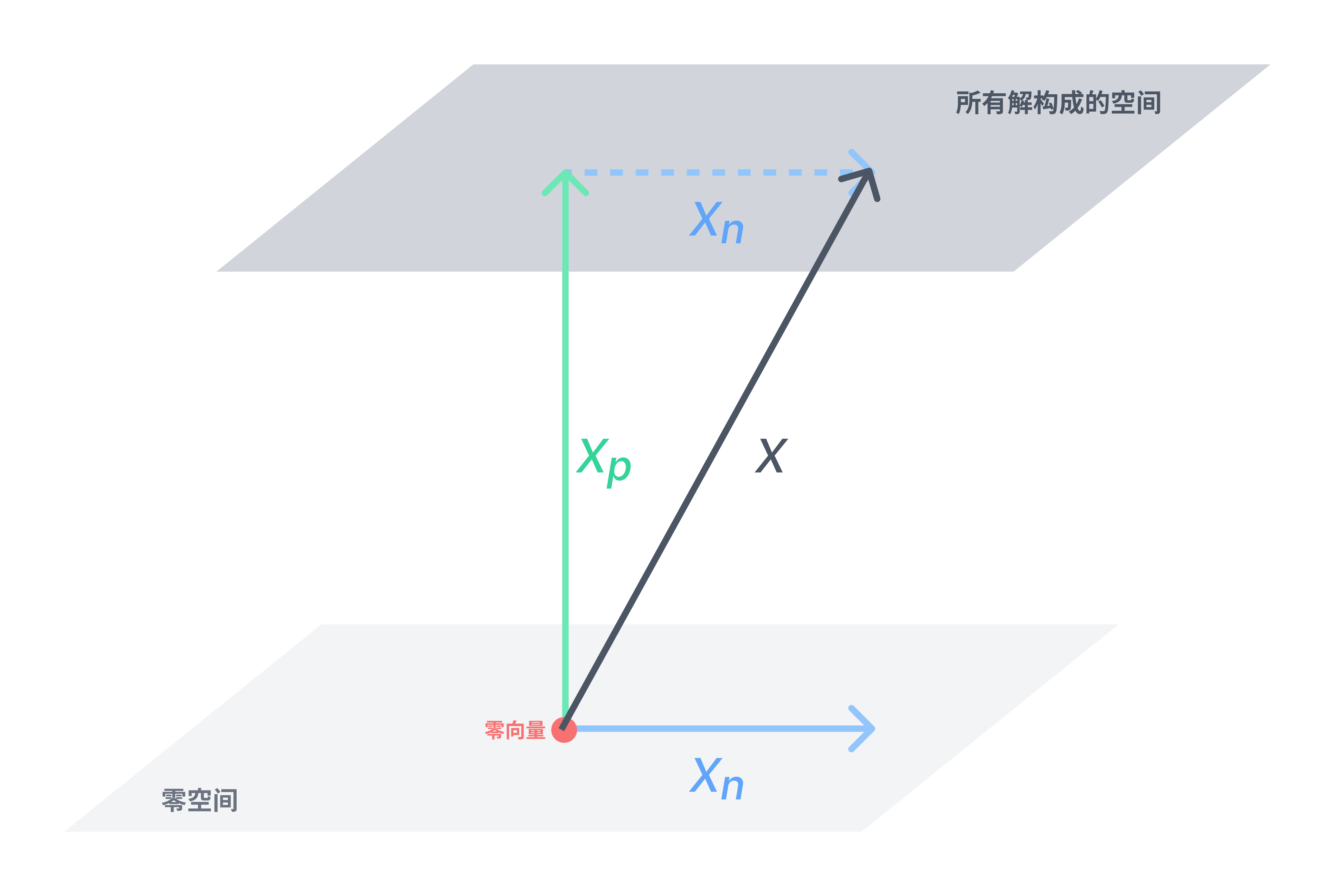 方程组的解所构成的空间
方程组的解所构成的空间
说明
由于行满秩,在简化行阶梯形式中系数矩阵不存在一整行的元素全为 的情况,而由于自由变量是可变动的,因此对于方程组 无论 取任意值都有解
当方程组的系数矩阵是一个方阵时,且列满秩(同时也就行满秩),即
例如方程组
消元法求解方程组
说明
此时方程组 有且只有 1 个解,其形式是
当不满秩 、 时,(类似于行满秩和列满秩的混合情况)此时方程组 有 0 个或无数个解,可解性由 决定。当有无数个解时,其形式是
在前面消元那一小节中,求解的方程组 得到了阶梯形式
所以该矩阵并不满秩
根据前一小节对可解性的讨论可知,在不满秩情况下,方程组是否有解由 决定
观察这个示例的增广矩阵,它的最后一行的 可使得等式成立,因此该方程组有无数个解
- 求出特解
令所有自由变量为
回代入增广矩阵可得
可得其中一个特解
- 以方程组 的零空间 作为基础解系
求出系数矩阵的简化行阶梯形式
根据
先将简化行阶梯形式 进行改写
即
可得
因此方程组 的两个特解是(相应地需要调换位置以对应原向量中 和 的顺序)
因此方程组 的解所构成的零空间是
提示
方程组 的零空间维度为 2,需要两个特解张成
将方程组 一个特定的解 和方程组 的所有解 结合,就是方程组 的通解,即满足以下等式
即对于方程组 , 其中 ,它有无数个解,其任意解/通解的形式是
