L20-克拉默法则、逆矩阵、体积

参考

Unit II: Least Squares, Determinants and Eigenvalues - Cramer's Rule, Inverse Matrix and Volume | pdf
课本章节：Read Section 5.3 in the 4^th or 5^th edition.
练习题：L20-克拉默法则、逆矩阵、体积-习题集

这一节课主要介绍行列式的应用：

逆矩阵 $A^{-1}$ 的表达式
方程组 $Ax=b$ 的解使用克拉默法则的表达式
行列式与面积和体积的关系

逆矩阵的表达式

在之前的课程中介绍了求解逆矩阵 $A^{-1}$ 的算法步骤

对于一个 $2 \times 2$ 的可逆矩阵 $A$

A= \begin{bmatrix} a & b \\ c & d \end{bmatrix}

通过与相同维度的单位矩阵 $I$ 构成增广矩阵

\begin{bmatrix} \begin{array}{c:c} \begin{matrix} a & b \\ c & d \end{matrix} & \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \end{array} \end{bmatrix}

再使用消元矩阵对增广矩阵左侧的部分进行变换，使其转换为单位矩阵：

通过 ${\color{Orange}d } \times {\color{Red}row1 } - {\color{Violet}b } \times {\color{Blue}row2 }$ 消元变换，再除以相减的差值，可以将左侧矩阵的第一行变成单位矩阵的第一行
通过 ${\color{Violet}a } \times {\color{Blue}row2 } - {\color{Orange}c } \times {\color{Red}row1 }$ 消元变换，在除以相减的差值，可以将左侧矩阵的第二行变成单位矩阵的第二行

\begin{aligned} \begin{bmatrix} \begin{array}{c:c} \begin{matrix} {\color{Red}a } & {\color{Red}b } \\ {\color{Blue}c } & {\color{Blue}d } \end{matrix} & \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \end{array} \end{bmatrix} \Rightarrow \begin{bmatrix} \begin{array}{c:c} \begin{matrix} {\color{Red}a }{\color{Orange}d } - {\color{Violet}b }{\color{Blue}c } & {\color{Red}b }{\color{Orange}d } - {\color{Violet}b }{\color{Blue}d } \\ {\color{Violet}a }{\color{Blue}c } - {\color{Red}a }{\color{Orange}c } & {\color{Violet}a }{\color{Blue}d } - {\color{Red}b }{\color{Orange}c } \end{matrix} & \begin{matrix} {\color{Orange}d } & -{\color{Violet}b } \\ -{\color{Orange}c } & {\color{Violet}a } \end{matrix} \end{array} \end{bmatrix} \\ \Rightarrow \begin{bmatrix} \begin{array}{c:c} \begin{matrix} {\color{Red}a }{\color{Orange}d } - {\color{Violet}b }{\color{Blue}c } & 0 \\ 0 & {\color{Violet}a }{\color{Blue}d } - {\color{Red}b }{\color{Orange}c } \end{matrix} & \begin{matrix} {\color{Orange}d } & -{\color{Violet}b } \\ -{\color{Orange}c } & {\color{Violet}a } \end{matrix} \end{array} \end{bmatrix} \\ \Rightarrow \begin{bmatrix} \begin{array}{c:c} \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} & \begin{matrix} \cfrac{{\color{Orange}d }}{ad-bc} & \cfrac{-{\color{Violet}b }}{ad-bc} \\ \cfrac{-{\color{Orange}c }}{ad-bc} & \cfrac{{\color{Violet}a }}{ad-bc} \end{matrix} \end{array} \end{bmatrix} \end{aligned}

则增广矩阵右侧部分就是逆矩阵

\begin{bmatrix} \cfrac{d}{ad-bc} & \cfrac{-b}{ad-bc} \\ \cfrac{-c}{ad-bc} & \cfrac{a}{ad-bc} \end{bmatrix}

提取出矩阵中各元素的公因数可以得到逆矩阵 $A^{-1}$ 更简洁的表达式

A^{-1}=\cfrac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}

观察以上 $2 \times 2$ 矩阵 $A$ 的逆矩阵的代数表达式，可以发现一些特点：

逆矩阵的表达式中各元素的公因数，其分母 $ad-bc$ 正好是矩阵 $A$ 的行列式 $detA$
逆矩阵的表达式中矩阵部分
- 其中 $(1, 1)$ 元素 $d$ 正好是矩阵 $A$ 的 $(1, 1)$ 元素的代数余子式
- 而 $(1, 2)$ 元素 $-b$ 正好是矩阵 $A$ 的 $(2, 1)$ 元素的代数余子式
- 而 $(2, 1)$ 元素 $-c$ 正好是矩阵 $A$ 的 $(1, 2)$ 元素的代数余子式
- 而 $(2, 2)$ 元素 $d$ 正好是矩阵 $A$ 的 $(2, 2)$ 元素的代数余子式
即逆矩阵的表达式中矩阵部分的各元素可以用原矩阵 $A$ 相应的代数余子式表达，元素的位置呈转置关系
如果将矩阵 $A$ 各元素相应的代数余子式，构成一个新的矩阵 $C$ 称为余子式矩阵，那么它的转置 $C^{T}$ 称为伴随矩阵

可以使用矩阵 $A$ 的行列式及相关表达式，得到逆矩阵 $A^{-1}$ 的代数表达式的更简化的版本

A^{-1}=\cfrac{1}{detA}C^{T}

其中 $detA$ 是矩阵 $A$ 的行列式，矩阵 $C^{T}$ 各元素都是由矩阵 $A$ 相应位置的元素的代数余子式构成，并进行转置得到

以上所得的公式也适用于高维度的矩阵，所以它是逆矩阵 $A^{-1}$ 的通用代数表达式

证明

要证明 $A^{-1}=\cfrac{1}{detA}C^{T}$ 公式成立

根据可逆矩阵的特性/定义 $AA^{-1}=I$ 并代入需要证明的公式

AA^{-1}=I \Leftrightarrow A\cfrac{1}{detA}C^{T}=I \Leftrightarrow AC^{T}=(detA)I

即相当于要证明 $AC^{T}=(detA)I$

其中 $C$ 是由矩阵 $A$ 各元素相应的代数余子式所构成的

$A$ 和 $C^{T}$ 之间存在特别的关系，它们的乘积/结果矩阵 $R$ 会有特别的结构（以矩阵与矩阵相乘的标准方法来考虑，左乘矩阵的行向量与右乘矩阵的列向量相乘得到结果矩阵的相应元素）

AC^{T}= \begin{bmatrix} a_{11} & \dots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix} \begin{bmatrix} C_{11} & \dots & C_{n1} \\ \vdots & \ddots & \vdots \\ C_{1n} & \dots & C_{nn} \end{bmatrix} =R

先观察结果矩阵 $R$ 的对角线上的元素，例如 ${\color{Orange} (1, 1)}$ 元素 ${\color{Orange} r_{11}}$ 是由矩阵 $A$ 的第一行与矩阵 $C^{T}$ 的第一列相乘而得的

AC^{T}= \begin{bmatrix} {\color{Red}a_{11} } & {\color{Red}\dots } & {\color{Red}a_{1n} } \\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix} \begin{bmatrix} {\color{Blue}C_{11} } & \dots & C_{n1} \\ {\color{Blue}\vdots } & \ddots & \vdots \\ {\color{Blue}C_{1n} } & \dots & C_{nn} \end{bmatrix}= \begin{bmatrix} {\color{Orange}r_{11} } & \dots & r_{1n} \\ \vdots & \ddots & \vdots \\ r_{n1} & \dots & r_{nn} \\ \end{bmatrix} =R

即 ${\color{Orange}r_{11} }=\sum_{j=1}^{n}{\color{Red}a_{1j} }{\color{Blue}C_{1j} }$

而以上 ${\color{Orange}r_{11} }$ 的公式正好就是矩阵 $A$ 行列式的表达式（含有代数余子式形式，以第一行的元素 $a_{1j}$ 作为公因数），所以该元素的结果等于矩阵 $A$ 的行列式 ${\color{Orange}r_{11} }=detA$

类似地，对于 $AC^{T}$ 的结果矩阵的对角线上的其他元素，也可以得到类似的公式，所以对角线上的元素都等于矩阵 $A$ 的行列式 ${\color{Orange}r_{ii} }=detA$

然后再观察结果矩阵 $R$ 的非对角线上的元素，例如 ${\color{Orange} (2, 1)}$ 元素 ${\color{Orange} r_{21}}$ 是由矩阵 $A$ 的第二行与矩阵 $C^{T}$ 的第一列相乘而得的

AC^{T}= \begin{bmatrix} a_{11} & \dots & a_{1n} \\ {\color{Red}a_{21} } & {\color{Red}\dots } & {\color{Red}a_{2n} } \\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix} \begin{bmatrix} {\color{Blue}C_{11} } & \dots & C_{n1} \\ {\color{Blue}C_{12} } & \dots & C_{n2} \\ {\color{Blue}\vdots } & \ddots & \vdots \\ {\color{Blue}C_{1n} } & \dots & C_{nn} \end{bmatrix}= \begin{bmatrix} r_{11} & \dots & r_{1n} \\ {\color{Orange}r_{21} } & \dots & r_{2n} \\ \vdots & \ddots & \vdots \\ r_{n1} & \dots & r_{nn} \\ \end{bmatrix} =R

即 ${\color{Orange}r_{21} }=\sum_{j=1}^{n}{\color{Red}a_{2j} }{\color{Blue}C_{1j} }$

以上的表达式与行列式（含有代数余子式形式）很类似，但它不是矩阵 $A$ 的行列式，因为如果以第二行元素 $a_{2j}$ 作为公因数，那么它们相乘的代数余子式应该是 $C_{2j}$

其实以上表达式可以是另一个矩阵 $A^{'}$ 的行列式（含有代数余子式形式），该矩阵 $A^{'}$ 和原矩阵 $A$ 很相似，只需要将矩阵 $A$ 的第二行复制替换它的第一行即可构建出来

A^{'}= \begin{bmatrix} {\color{Red}a_{21} } & {\color{Red}\dots } & {\color{Red}a_{2n} } \\ {\color{Red}a_{21} } & {\color{Red}\dots } & {\color{Red}a_{2n} } \\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix}

在计算两个矩阵的行列式 $detA$ 和 $detA^{'}$ 时，如果两个矩阵都选取第一行的元素作为公因数，那么两个矩阵行列式的表达式中，相应的代数余子式都是一样的，即 $C_{1j}=C^{'}_{1j}$

由于矩阵 $A$ 和矩阵 $A^{'}$ 的区别仅是第一行不同，而第一行元素所对应的代数余子式，都是由删去第一行和相应列元素后，剩下的元素所构成的 $(n-1) \times (n-1)$ 矩阵的行列式

所以矩阵 $A$ 和 $A^{'}$ 的第一行元素所对应的代数余子式都是一样的

同时由于矩阵 $A^{'}$ 的第一行和第二行元素相等

所以表达式 ${\color{Orange}r_{21} }=\sum_{j=1}^{n}{\color{Red}a_{2j} }{\color{Blue}C_{1j} }$ 对于矩阵 $A^{'}$ 而言，可以转换为 ${\color{Orange}r_{21} }=\sum_{j=1}^{n}{\color{Red}a_{2j} }{\color{Blue}C_{1j} }=\sum_{j=1}^{n}a_{1j}C^{'}_{1j}$ 该表达式正好是矩阵 $A^{'}$ 的行列式（选区第一行的元素作为公因数），由于矩阵 $A^{'}$ 存在两行相同（第一行和第二行），根据行列式的特性四可知 $detA^{'}=0$

所以 ${\color{Orange}r_{21} }=\sum_{j=1}^{n}{\color{Red}a_{2j} }{\color{Blue}C_{1j} }=\sum_{j=1}^{n}a_{1j}C^{'}_{1j}=detA^{'}=0$

即 $AC^{T}$ 结果矩阵 $R$ 的 $(2, 1)$ 元素 $r_{21}$ 可以看作是矩阵 $A^{'}$ 的行列式 $detA^{'}$ ，而这个矩阵的行列式为 $0$

对于其他非对角线上的元素，都可以使用类似的方式，根据表达式构建出相应的矩阵，让这些元素（表达式）成为这些矩阵的行列式（含有代数余子式）的表达式，而且这些矩阵的行列式都是 $0$

所以 $AC^{T}$ 的结果矩阵在对角线上的元素都是 $detA$ ，而非对角线上的元素都是 $0$

可以证得

AC^{T}= \begin{bmatrix} detA & 0 & 0 & \dots & 0 \\ 0 & detA & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & detA \end{bmatrix} =detA \begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \end{bmatrix} =(detA)I

克拉默法则

求解方程组 $Ax=b$ 如果矩阵 $A$ 是可逆矩阵时，那么方程组有解为 $x=A^{-1}b$

将上一小节所得的逆矩阵的代数表达式代入，可得方程组的解为

x=\cfrac{1}{detA}C^{T}b

其中 $detA$ 是矩阵 $A$ 的行列式， $C^{T}$ 是伴随矩阵（其中的元素是由矩阵 $A$ 的各元素相应的代数余子式构成的，再进行转置）， $b$ 是列向量

克拉默法则可以将以上表达式进行「拆解」，得到解的另一种形式，给出 $x=\begin{bmatrix} x_{1} \\ \vdots \\ x_{j} \\ \vdots \\ x_{n} \end{bmatrix}$ （列向量）中的每一个元素 $x_{j}$ 的表达式

x_{j}=\cfrac{detB_{j}}{detA}

而其中矩阵 $B_{j}$ 是用向量 $b$ 替换了矩阵 $A$ 第 $j$ 列所得到的矩阵

例如 $B_{1}$ 就是用向量 $b$ 替换了矩阵 $A$ 的第一列后所得的矩阵

证明

方程组的解

x=\cfrac{1}{detA}C^{T}b

其中 $C^{T}$ 是伴随矩阵，它的元素是由矩阵 $A$ 的各元素相应的代数余子式构成的，再进行转置而得到的

C^{T}= \begin{bmatrix} C_{11} & C_{{\color{Red}21 }} & \dots & C_{n1} \\ C_{{\color{Red}12 }} & C_{22} & \dots & C_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ C_{1n} & C_{2n} & \dots & C_{nn} \end{bmatrix}

而 $b$ 是列向量

b= \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{bmatrix}

所以在方程组的解就是（矩阵与列向量相乘）

\begin{aligned} x&=\cfrac{1}{detA}C^{T}b \\ &=\cfrac{1}{detA} \begin{bmatrix} C_{11} & C_{21} & \dots & C_{n1} \\ C_{12} & C_{22} & \dots & C_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ C_{1n} & C_{2n} & \dots & C_{nn} \end{bmatrix} \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{bmatrix} \\ &=\cfrac{1}{detA} \begin{bmatrix} C_{11}b_{1}+C_{21}b_{2}+\dots+C_{n1}b_{n} \\ C_{12}b_{1}+C_{22}b_{2}+\dots+C_{n2}b_{n} \\ \vdots \\ C_{1n}b_{1}+C_{2n}b_{2}+\dots+C_{nn}b_{n} \end{bmatrix} \\ &= \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} \end{aligned}

所以对于解（列向量）的第一个元素 $x_{1}=\cfrac{1}{detA}(C_{11}b_{1}+C_{21}b_{2}+\dots+C_{n1}b_{n})$

观察其中相加的部分 $C_{11}b_{1}+C_{21}b_{2}+\dots+C_{n1}b_{n}$ 它结构是代数余子式和相应的 $b_{j}$ 元素相乘，很像矩阵行列式的形式

由于伴随矩阵 $C^{T}$ 里面的元素都是矩阵 $A$ 的代数余子式，但是上面的表达式中相乘的元素不是矩阵 $A$ 的元素 $a_{j}$ 而是向量 $b$ 的元素

所以可以根据矩阵 $A$ ，使用向量 $b$ 替换其中的某一列，构造出一个新的矩阵 $B$ ，使得上面的表达式正好是它的行列式（含有代数余子式）的表达式

观察第一个元素 $x_{1}$ 的表达式，由于代数余子式的列下标都是 $1$

所以该表达式可以看作是选取了矩阵 $B$ 的第一列作为公因数，而这一列的元素由（列）向量 $b$ 构成（即用列向量 $b$ 替换了矩阵 $A$ 的第一列，而其他列的元素都是和 $A$ 一样）

B_{1}= \begin{bmatrix} {\color{Blue}b_{1} } & a_{12} & \dots & a_{1n} \\ {\color{Blue}b_{2} } & a_{22} & \dots & a_{2n} \\ {\color{Blue}\vdots } & \vdots & \ddots & \vdots \\ {\color{Blue}b_{n} } & a_{n2} & \dots & a_{nn} \end{bmatrix}

那么第一列的各元素 $b_{j}$ 乘上相应的代数余子式 $C_{j1}$ ，再求和就得到了矩阵的行列式（这里是可以选取矩阵的某一列的元素作为公因数，而不是某一行，因为根据行列式的特性十，转置矩阵的行列式和原来矩阵的行列式一样）

所以第一个元素 $x_{1}$ 是矩阵 $B_{1}$ 的行列式

类似地，可以根据 $x_{j}$ 的表达式，推导出 $B_{j}$ 的结构，即用向量 $b$ 替换了矩阵 $A$ 第 $j$ 列

不推荐

对于方程组 $Ax=b$ ，可以根据克拉默法则 $x_{j}=\cfrac{detB_{j}}{detA}$ 分别求出解 $\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix}$ 的各元素的值，从而求解方程组

但是观察克拉默法则的公式，实际上需要分别求解 $detA$ 和 $n$ 个 $detB_{j}$ ，共 $(n+1)$ 个矩阵的行列式

而如果行列式是使用通用公式进行求解的，那么每个行列式都需要进行 $n!$ 项求和（每项都是 $n$ 个元素相乘）

所以使用克拉默法则求解方程组 $Ax=b$ 运算量其实很大，其效率比消元求解的算法更繁琐，并不推荐

体积

提示

通过坐标系（向量）可以将几何图形与线性代数联系起来，其中几何形状的面积和体积对应于矩阵的行列式

该矩阵是基于几何图形的顶点坐标（作为矩阵的元素）所构建出来的（或以几何的边作为向量，再基于向量构建矩阵）

如果将 $3 \times 3$ 的矩阵的各行的向量作为边（各列向量作为边也是一样的）

A= \begin{bmatrix} {\color{Red}a_{11} } & {\color{Red}a_{12} } & {\color{Red}a_{13} } \\ {\color{Blue}a_{21} } & {\color{Blue}a_{22} } & {\color{Blue}a_{23} } \\ {\color{Green}a_{31} } & {\color{Green}a_{32} } & {\color{Green}a_{33} } \end{bmatrix}

在空间坐标系中构成一个「盒子」 box（平行六面体）

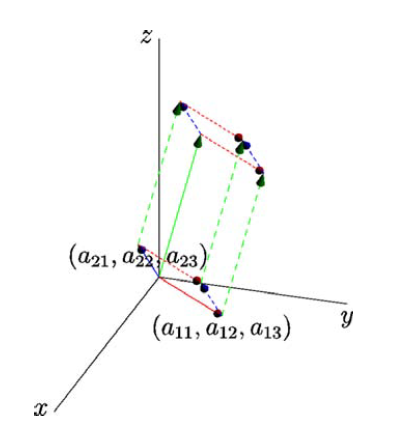
那么盒子的体积就是该矩阵行列式的绝对值

V_{box}=\left | detA \right |

有多种方法证明以上的说法，课程通过证明这个平行六面体的体积也具有行列式的 3 个基础特性（只需要证明这 3 个基础特性，既可以推导出符合其余的 7 个特性），从而证得体积和行列式（的绝对值）是等价的

疑问

以上的证明方式并不是从几何性质入手，是否通过数理性质相同来证得两者相同呢？

以下证明体积也具有/满足行列式的 3 个基础特性：

如果矩阵是单位矩阵 $A=I$
则构成一个正方体（而且边长为 $1$ ），该正方体的体积为 $1$ ；此时矩阵的行列式为 $detA=1$
所以在矩阵是单位矩阵的情况下， $V_{box}=\left | detA \right |$ 成立，这就证明了该「盒子」的体积满足行列式的特性一
绝对值
请留意体积与行列式的对应关系里是存在绝对值的 $V_{box}=\left | detA \right |$
因为行列式的值可能为正，也可以为负，而「盒子」的体积必须是正值
如果这个 $3 \times 3$ 矩阵是一个正交矩阵 $Q$ ，即该矩阵由一系列标准正交向量构成，它们相互正交，模长为 $1$
那么该矩阵的体积也是 $V_{box}=1$ ，但是矩阵的行列式却是 $\pm 1$ （可能是 $1$ 也可能是 $-1$ ）
以下证明正交矩阵 $Q$ 的行列式 $detQ$ 为 $\pm 1$
已知正交矩阵满足 $Q^{T}Q=I$
对等式两边的矩阵同时求行列式，可得 $det(Q^{T}Q)=detI=1$
根据行列式的特性九可得
$det(Q^{T}Q)=detQ^{T}detQ=1$
再根据行列式的特性十可得
$detQ^{T}detQ=detQdetQ=(detQ)^{2}=1$
则可得
$detQ=\pm 1$
所以体积与行列式的对应关系中，需要存在绝对值 $V_{box}=\left | detA \right |$
如果交换矩阵的两行
则行列式的正负号改变；而使用矩阵的行向量作为边所构建的「盒子」（平行六面体），只是改变了它在三维空间中的位置，体积并不会改变
所以等式 $V_{box}=\left | detA \right |$ 依然成立，可以说「盒子」的体积满足行列式的特性二
如果增加矩阵其中一行数乘 $t$ （其他行保持不变）
则行列式会变成原来的 $t$ 倍；以矩阵的行向量作为边所构建的「盒子」（平行六面体），相应地其中一边的边长也会增加 $t$ 倍，那么这个平行六面体的体积也会增加 $t$ 倍
所以等式 $V_{box}=\left | detA \right |$ 依然成立，可以说「盒子」的体积满足行列式的特性三之一
如果矩阵的其中一行进行相加操作（其他行保持不变）
则所得的矩阵的行列式可以进行相应的拆分 $\begin{vmatrix} a+a^{\prime} & b+b^{\prime} \\ c & d \end{vmatrix}= \begin{vmatrix} a & b \\ c & d \end{vmatrix}+ \begin{vmatrix} a^{\prime} & b^{\prime} \\ c & d \end{vmatrix}$
提示
在课程中（包括课程的小结文稿和教材书籍的相应的章节中）并没有直接证明体积满足以上变换，而是通过证明平行四边形的面积符合以上变换
再提及这个变换可以扩展适用高维度，间接证明了体积满足行列式的特性三之二

从几何（二维平面）的角度来观察这个变换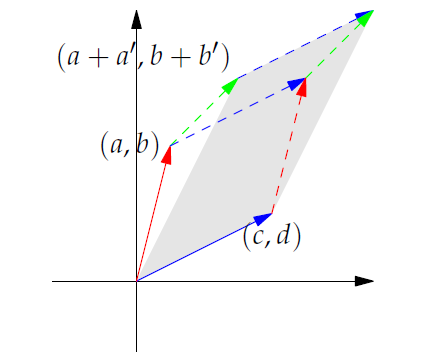
平面满足行列式的特性三之二

由向量 ${\color{Red}(a, b) }$ 和 ${\color{Blue}(c, d) }$ 所构成的平行四边形 $S_{1}$
由向量 ${\color{Lime}(a, b) }$ 和 ${\color{Blue}(c, d) }$ 所构成的平行四边形 $S_{2}$
由向量 ${\color{Gray}(a+a^{'}, b+b^{'}) }$ 和 ${\color{Blue}(c, d) }$ 所构成的平行四边形（灰色阴影部分）的面积 $S_{3}$
三者之间满足 $S_{1}+S_{2}=S_{3}$
所以平行四边形的面积满足行列式的特性三之二，可以这个变换可以扩展适用高维度，即平行六面体的体积满足行列式的特性三之二

以上证明了由 $3 \times 3$ 矩阵的各行的向量作为边所构成的平行六面体，其体积满足行列式的 3 个基础特性，所以证得 $V_{box}=\left | detA \right |$ 成立

面积

通过坐标系（向量）可以将平行四边形与线性代数联系起来

如果平行四边形由两个列向量 $\begin{bmatrix} a \\ b \end{bmatrix}$ 和 $\begin{bmatrix} c \\ d \end{bmatrix}$ 构成（它们分别相交于直角坐标系的零点）

由这两个列向量构成的矩阵

\begin{bmatrix} a & c \\ b & d \end{bmatrix}

那么平行四边形的面积就是所构造的矩阵的行列式 $S=ad-cd$

相应地，如果由这两个向量构成的是三角形，那么面积是 $S=\cfrac{1}{2}(ad-cd)$

以上的几何图形的其中一个顶点位于零点（两个向量相交于零点），如果两个向量的交点不在零点，则所构造的矩阵会有所不同

例如三角形的三个顶点的坐标分别是 $(x_{1}, y_{1})$ 、 $(x_{2}, y_{2})$ 、 $(x_{3}, y_{3})$ 构建出相应的矩阵

\begin{bmatrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{bmatrix}

可以通过求解矩阵的行列式，得到三角形的面积

S= \cfrac{1}{2} \begin{vmatrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{vmatrix}