显著性

统计显著性 statistical significance

使用置信区间和假设检验，你能够在做决策时提供统计显著性。

实际显著性 practical significance

实际显著性考虑到所处情况（现实环境）的其他因素（更现实），假设检验或置信空间的结果可能不会直接考虑到这种情况。空间、时间或金钱等约束条件对商业决定很重要。但是可能不会在统计测试中直接考虑这些因素。

p 值

根据预设的零假设，模拟获得的（正态）分布中，p 值的定义是：如果零假设为真，观察到统计量（或支持备择假设的更多极端）的概率，即舍弃预设的零假设，接受备着假设的概率。

根据大数定理和中心极限定理，由零假设模拟产生的正态分布，其均值为中心对称点，而观测到的统计量结合图像上来看 p 值，即图形的相关的阴影分为三种情况：

如果参数大于备择假设中的某个数值，为了得到 p 值，你的阴影可能是这样的：
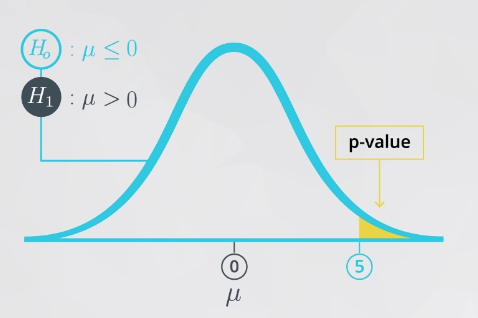
μ>0
如果参数小于备择假设中的某个数值，为了得到 p 值，你的阴影可能是这样的：
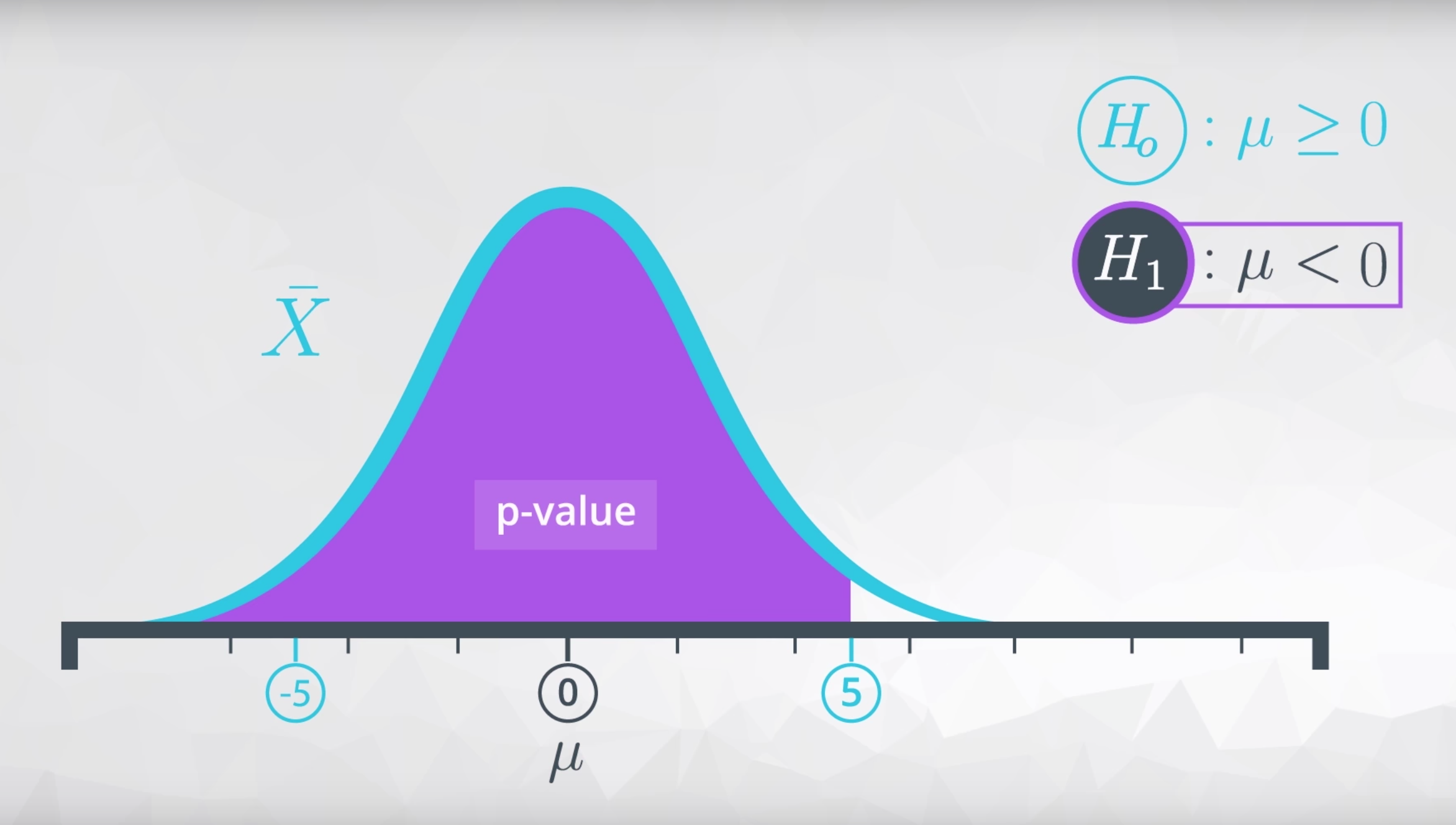
μ<0
如果参数不等于备择假设中的某个数值，为了得到 p 值，你的阴影可能是这样的：
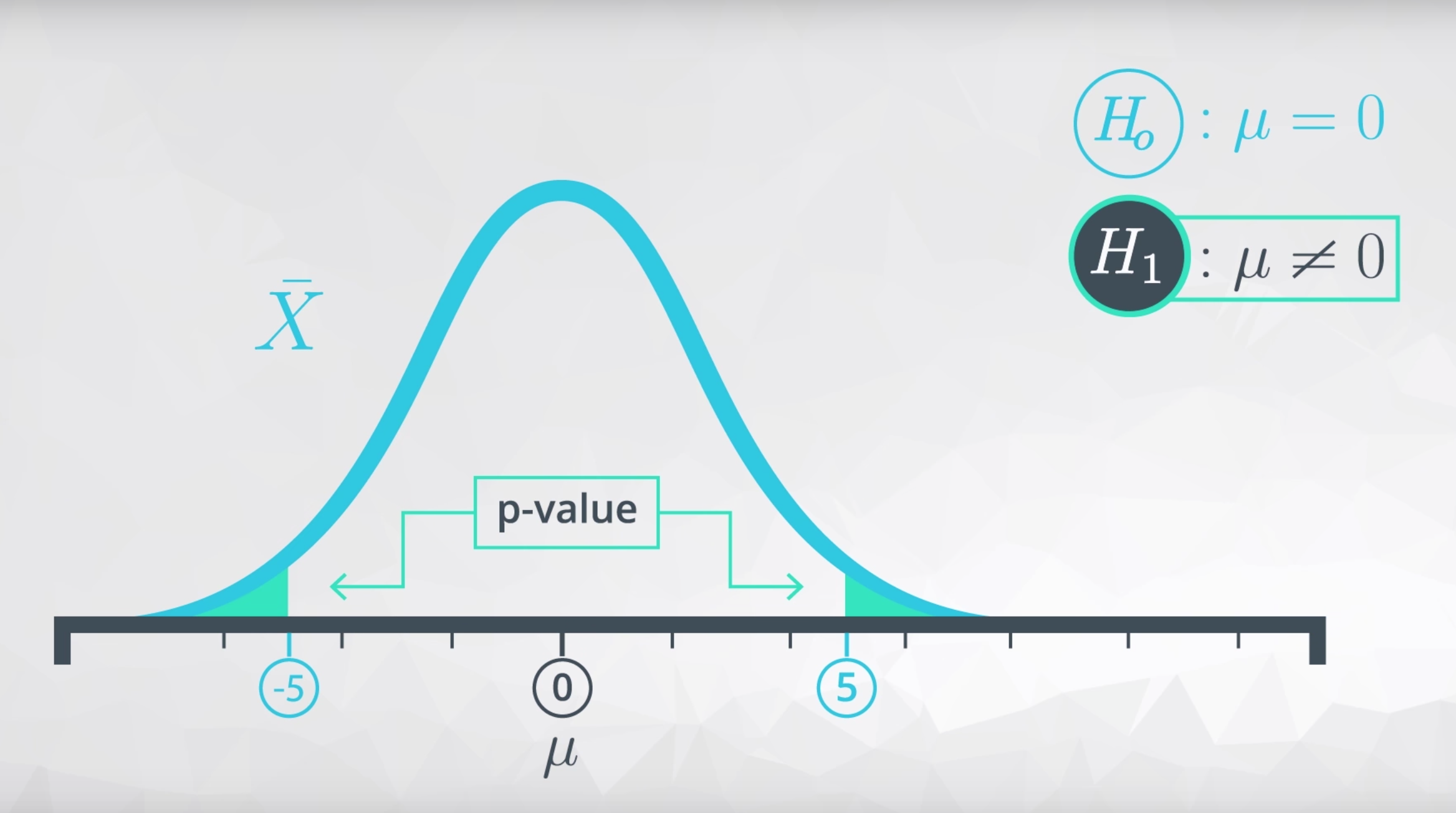
μ≠0

三种情况的阴影面积大小都是表征了模拟的量和观测到的统计量关系

计算 p 值

根据备择假设的预设值使用函数 np.random.normal(loc=0.0, scale=1.0, size=None) 模拟出统计量（的均值）抽样分布

参数 loc 是零假设中预设的均值（取等号时的值）
参数 scale 根据实际样本数据计算的抽样分布标准差
参数 size 一般设定为 10000（输出尽量多的模拟采样数据以模拟正态分布）

python

null_sims= np.random.normal(null_hypo_mean, np.std(means), 1000)

绘出基于零假设的模拟抽样分布 null_sims 和观测值 sample_mean

python

plt.hist(null_sims);
plt.axvline(x=sample_mean, color='red');

利用模拟的统计量 null_sims 与样本观察得到的统计量 sample_mean，基于备择假设的类型作差，求得 $p$ 值（阴影面积）

sample_mean 是指实际样本数据的平均值（观测值）sample_mean = sample.mean()

python

# 左侧阴影，即备择假设为 μ < sample_mean
# null_vals 是模拟获得的**样本平均值抽样分布的变量**
(null_sims < sample_mean).mean()

# 右侧阴影，即备择假设为 μ > sample_mean
(null_sims > sample_mean).mean()

# 双侧阴影，即备择假设 μ ≠ sample_mean
# null_mean 是模拟获得的**样本平均值抽样分布的均值**（即正态分布的对称点横坐标）
low_ext = (null_mean - (sample_mean - null_mean))   # 下界
high_ext = sample1.height.mean()   # 上界

(null_sims < low_ext).mean() + (null_sims > high_ext).mean()

选择假设

当 p 值较小（ $< 0.05$ 或 $< 0.01$ ）时，表征零假设预设得到的模拟值与观测值相差较远，应该舍弃零假设，接受备择假设
当 p 值较大（ $> 0.05$ ）时，表征零假设预设得到的模拟值与观测值距离较近，即零假设下模拟的分布可以较高可能性获得观测值，舍弃备择假设

Announce

选择哪一个假设是基于 $p$ 值的，设定 $p$ 值大小会与 I 类错误阈值 $\alpha$ 密切相关

$pval \leq \alpha \Rightarrow$ 拒绝 $H_0$
$pval > \alpha \Rightarrow$ 不拒绝 $H_0$